 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Показатели формы распределения
Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). Число наблюдений, по которому строится эмпирическое распределение, обычно невелико и представляет собой выборку из исследуемой генеральной совокупности. Поэтому эмпирические данные в определенной степени связаны со случайными ошибками наблюдения, величина которых неизвестна. С увеличением числа наблюдений и одновременным уменьшением величины интервала зигзаги полигона начинают сглаживаться, и в пределе мы приходим к плавной кривой, которая называется кривой распределения. Кривая распределения характеризует теоретическое распределение, т.е. то распределение, которое получилось бы при полном погашении всех случайных причин, затемняющих основную закономерность. В практике статистического исследования приходится встречаться с самыми различными распределениями. Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны междусобой.Для симметричных распределений имеет место равенство средней арифметической, моды и медианы. Величина показателя асимметрии
Рис. 5.1. Асимметричные ряды распределения: 1 – с правосторонней асимметрией; 2 – с левосторонней асимметрией
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):
где
Применение этого показателя дает возможность не только определить степень асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений и рассчитывается по формуле Если отношение Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Наиболее точным является показатель, основанный на использовании центрального момента четвертого порядка:
где
 . .

Рис. 5.2. Ряды распределения с положительным (a) и отрицательным (б) эксцессом
На рис. 5.2 представлены два распределения: одно – островершинное (величина эксцесса положительная), второе – плосковершинное (величина эксцесса отрицательная). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Эксцесс может быть положительным и отрицательным. У высоковершинных распределений показатель эксцесса имеет положительный знак (+), а у низковершинных – отрицательный знак (–). Предельным значением отрицательного эксцесса является значение В нормальном распределении отношение Средняя квадратическая ошибка эксцесса рассчитывается по формуле
где п – число наблюдений. Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения.
Кривые распределения
Наиболее надежный путь выявления закономерностей распределения – увеличение количества наблюдений. По мере увеличения количества наблюдений (в пределах той же однородной совокупности) при одновременном уменьшении величины интервала закономерность, характерная для данного распределения, будет выступать все более и более ясно, а представляющая полигон частот ломаная линия будет приближаться к некоторой плавной линии и в пределе должна превратиться в кривую линию. Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения. В практике статистических исследований часто используется распределение Пуассона, Максвелла, особенно нормальное распределение. Распределения, близкие к нормальному распределению, были обнаружены при изучении самых различных явлений как в природе, так и в развитии общества. В статистической практике большой интерес представляет решение вопроса о том, в какой мере можно считать полученное в результате статистического наблюдения распределение признака в исследуемой совокупности соответствующим нормальному распределению. Для решения этого вопроса следует рассчитать теоретические частоты нормального распределения, т.е. те частоты, которые были бы, если бы данное распределение в точности следовало закону нормального распределения. Для расчета теоретических частот применяется следующая формула:
где t – нормированное отклонение: Следовательно, в зависимости от величины t для каждого интервала эмпирического ряда определяются теоретические частоты. Для проверки близости теоретического и эмпирического распределений используются специальные показатели, называемые критериями согласия.Наиболее распространенным является критерий согласия К. Пирсона
где f – эмпирические частоты (частости) в интервале; Полученное значение критерия ( Если При расчете критерия Пирсона необходимо соблюдать условия: число наблюдений должно быть достаточно велико (п > 50); если теоретические частоты в некоторых интервалах меньше 5, то интервалы объединяют так, чтобы частоты были больше 5.
Контрольные вопросы для самопроверки
1. Что представляет собой вариация признака и в чем состоит значение ее изучения? 2. Какие показатели вариации находят наиболее широкое применения? 3. Что такое размах вариации, по какой формуле он исчисляется? 4. Какой показатель вариации называется дисперсией? По каким формулам она рассчитывается? 5. Каковы основные свойства дисперсии? 6. Что собой представляет правило сложения дисперсий, в чем его практическое значение? 7. Напишите соотношение между показателями центра распределения при правосторонней и левосторонней асимметрии. 8. В чем состоит значение проверки гипотезы о форме распределения? 9. Каковы особенности кривых нормального распределения? Их использование в анализе фактических данных. 10. Какие критерии согласия используются наиболее часто?
ГЛАВА 6. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Поиск по сайту: |
 может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии (правая ветвь относительно максимальной ординаты вытянута больше – чем левая, рис. 5.1). При правосторонней асимметрии между показателями центра распределения существует соотношение:
может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии (правая ветвь относительно максимальной ординаты вытянута больше – чем левая, рис. 5.1). При правосторонней асимметрии между показателями центра распределения существует соотношение:  . Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии
. Отрицательный знак показателя асимметрии свидетельствует о наличии левосторонней асимметрии  .
.

 ,
, – центральный момент третьего порядка:
– центральный момент третьего порядка: .
. , где n – число наблюдений.
, где n – число наблюдений. , асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если отношение
, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если отношение  , асимметрия несущественна.
, асимметрия несущественна. ,
, – центральный момент четвертого порядка:
– центральный момент четвертого порядка: = –2, величина положительного эксцесса является величиной бесконечной.
= –2, величина положительного эксцесса является величиной бесконечной.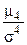 = 3. Следовательно, для нормального закона
= 3. Следовательно, для нормального закона  = 0.
= 0. ,
, ,
, .
. («хи - квадрат»), вычисляемый по формуле
(«хи - квадрат»), вычисляемый по формуле ,
, – теоретические частоты (частости) в интервале.
– теоретические частоты (частости) в интервале. ) сравнивается с табличным значением (
) сравнивается с табличным значением (  ) в зависимости от принятой вероятности и числа степеней свободы k (для нормального распределения k равно числу групп в ряду распределения минус 3).
) в зависимости от принятой вероятности и числа степеней свободы k (для нормального распределения k равно числу групп в ряду распределения минус 3).