 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГЛАВА 4. АБСОЛЮТНЫЕ, ОТНОСИТЕЛЬНЫЕ И СРЕДНИЕ
СТАТИСТИЧЕСКИЕ ВЕЛИЧИНЫ Абсолютные статистические величины Статистические величины – это некоторая количественная категория, с помощью которой измеряются явления общественной жизни. Статистические величины бывают абсолютными, относительными и средними. Абсолютными статистическими величинами называются показатели, выражающие размеры, объемы и уровни общественных явлений и процессов. По способу выражения абсолютные величины подразделяются на индивидуальные и суммарные. Индивидуальные показатели – показатели, выражающие размеры количественных признаков отдельных единиц исследуемых объектов (например, выработка определенного рабочего за месяц и т.д.). Суммарные показатели выражают величину того или иного признака всех единиц изучаемой совокупности (выработка всех рабочих за месяц). Абсолютная статистическая величина – это число, имеющее название и размерность. В экономической статистике абсолютные величины делят на 3 категории: натуральные, денежные (стоимостные), трудовые единицы измерения. Абсолютные статистические величины всегда являются именованными числами, т.е. выражаются в определенных единицах измерения: килограммах, метрах, штуках и т.д. Натуральные единицы могут быть простыми (тонны, штуки, литры, метры и т.п.) и сложными, являющимися комбинацией двух разноименных величин (грузооборот выражается в тонно-километрах, производство электричества – в киловатт-часах). В группу натуральных также входят условно-натуральные единицы измерения, которые используются в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 мДж/кг. Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Наиболее широко применяются денежные единицы измерения (рубли, доллары и т.д.). Они используются для характеристики разнородных явлений в едином стоимостном выражении. К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.
Относительные статистические величины Для того чтобы произвести полный анализ исследуемых явлений, определить их связи и закономерности, сделать определенные выводы, одних абсолютных величины недостаточно. В ходе экономического анализа возникает необходимость в сравнении и сопоставлениях. Результаты сравнения выражаются при помощи относительных величин. Относительная статистическая величина представляет собой отношение двух абсолютных величин. Величина, которая находится в числителе этого отношения, называется сравниваемой или отчетной величиной, а в знаменателе – базисной величиной или базой сравнения. Таким образом, относительная величина показывает, во сколько раз отчетная величина отличается от базисной, или какую долю отчетная величина составляет по сравнению с базисной. Относительная величина может выражаться в относительных величинах (безразмерная), в процентах (когда основание принимается за 100 %), в промилле (когда основание принимается за 1000). Иногда используют и другие основания, например, 10 тыс., 100 тыс. и т. д. Кроме того, бывают и именованные относительные величины. В частности, к ним относятся относительные величины интенсивности. Например, плотность населения в том или ином районе представляет собой отношение
По характеру назначения и сущности выражаемых количественных соотношений различают следующие виды относительных величин: структуры, динамики, планового задания и выполнения плана, интенсивности, сравнения. Относительные величины структуры характеризуют долю отдельных частей в общем объеме совокупности и выражаются в долях единицы или процентах. Получаются эти величины в результате деления значения каждой части совокупности на их общий итог, который принимается за базу сравнения. Каждую относительную величину структуры называют удельным весом. Cумма относительных величин структуры изучаемой совокупности должна быть равна 100 % или 1.
Пример 4.1. Рассмотрим табл. 4.1. Рассчитанные в последней графе табл. 4.1 проценты представляют собой относительные показатели структуры (в данном случае – удельные веса).
Таблица 4.1. Группировка промышленных предприятий по числу работников (чел)
Относительные величины динамики характеризуют изменение явления во времени. Они показывают, во сколько раз увеличился (или уменьшился) объем явления за определенный период времени, их называют коэффициентами роста. Коэффициенты роста, умноженные на 100, называются темпами роста. Относительная величина динамики – это отношение фактической (отчетной) величины показателя ( Например, инвестиции в экономику за счет всех источников финансирования составили в 2005 году 143,8 млрд. руб., а в 2004 г. – 152,0 млрд. руб. Относительная величина динамики равна Относительная величина планового задания – это отношение величины показателя по плану (yпл) к его фактической величине предшествующего периода ( Относительная величина выполнения плана – это отношение фактической величины показателя (y1) к запланированной на тот же период его величине (yпл), т.е. Например, в 2004 г. было произведено стиральных машин 6103 тыс. штук при плане 6481 тыс. штук. Относительная величина выполнения плана равна:
Следовательно, план недовыполнен на 5,8%. Относительные величины планового задания, выполнения плана и динамики связаны между собой следующим образом:
Относительные величины сравнения (наглядности) выражают сравнительные размеры одноименных величин, которые относятся к разным объектам по одному и тому же периоду времени. Например, сравнение годовой производительности труда по двум предприятиям или сопоставление данных о численности населения разных городов. Пример 4.2.[11]Территория Ставропольского края составляет 66,5 тыс. км2, а территория Ростовской области – 100,8 тыс. км2 . Коэффициент сравнения равен Относительная величина интенсивности получается в результате сопоставления двух разноименных абсолютных величин. В отличии от других относительных величин они являются именованными числами и показывают итог числителя, приходящийся на одну, на десять, на сто единиц знаменателя и т.д. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности и т.д. как отношение числа родившихся (умерших) к среднегодовой численности населения данной территории в расчете на 1000 человек. Или, плотность населения, выражающаяся средним числом жителей на одном квадратном метре территории, доходы на душу населения, потребление продукции на душу населения. Относительные величины координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на десятую или сто единиц другой группы изучаемой совокупности. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. Например, сколько служащих на предприятии приходится на 100 рабочих. Пример 4.3. Расход топлива на производственные нужды предприятия характеризуются в отчетном периоде следующими данными (табл. 4.2) [7].
Таблица 4.2. Расход топлива на производственные нужды предприятия
Средние калорийные эквиваленты (коэффициенты) перевода в условное топливо составили: мазут – 1,37 т, уголь – 0,9 т, газ – 1,2 тыс. м3. Определить: 1) общее потребление условного топлива по плану и фактически; 2) процент выполнения плана по общему расходу топлива; 3) удельные веса фактически израсходованного топлива по видам. Решение: 1. Для определения общего потребления топлива используем условно-натуральный метод. Расходы по плану и фактически исчисляются в единицах условного топлива (усл. ед.):
2. Процент выполнения плана по общему расходу топлива:
Следовательно, фактический расход топлива превысил плановый на 3,27 %. 3. Для определения удельного веса израсходованного топлива по видам (структуры расхода топлива) используем табл. 4.3.
Таблица 4.3. Фактический расход топлива
Следовательно, в отчетном периоде на производственные нужды предприятия было израсходовано всего 1810,4 усл. ед. топлива, при этом удельный вес мазута составил 39,4 %, угля – 14,9 %, газа природного – 45,7 %.
4.3. Средние величины
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени. Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности. Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности. В экономических исследованиях и плановых расчетах применяются две категории средних: • степенные средние; • структурные средние. К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Средняя обозначается через Общая формула степенной средней записывается следующим образом:
где fi – частота (повторяемость индивидуальных значений признака); хi – величины, по которым вычисляется средняя. В зависимости от степени k получаются различные виды средних величин, их формулы представлены в табл. 4.4.
Таблица 4.4. Формулы расчета различных видов степенных средних величин
Как видно из данных табл. 4.4, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т.е. умножают на нее. Частоты при этом называются статистическими весами или просто весами средней. В качестве веса могут применяться какие-либо другие величины (в табл. 4.4 они обозначены буквой W). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями (относительные частоты). Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени (k), не одинаковы. Чем больше показатель степени k, тем больше значение средней величины. Таким образом, выполняется правило мажорантности средних:
Какую среднюю вычислять – решается в каждом отдельном случае, исходя из задачи исследования и наличия исходной информации. Чаще всего используется средне арифметическая и средне гармоническая. Они используются в плановых расчетах, при расчете общей средней и средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Средняя арифметическая применяется в тех случаях, когда известны варианты варьирующего признака и их частот. Средняя арифметическая обладает следующими математическими свойствами: 1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
3. Если варианты значений признака уменьшить или увеличить на постоянное число A, то средняя арифметическая соответственно уменьшится или увеличится на эту величину: 4. Если все варианты значений уменьшить или увеличить в A раз, то средняя также соответственно увеличится или уменьшится в A раз:
5. Если все частоты уменьшить или увеличить в A раз, то средняя арифметическая от этого не изменится:
Пример 4.4. В бригаде из трех рабочих зарплата распределяется следующим образом: 1. Иванов – 3000 рублей 2. Петров – 3200 рублей. 3. Сидоров – 4000 рублей. Нужно определить среднюю зарплату в бригаде. Для решения задачи использовалась формула простой средней арифметической:
Пример 4.5. Распределение служащих фирмы по стажу работы представлено в табл. 4.5.
Таблица 4.5. Распределение рабочих участка по стажу работы
Определить средний стаж работы рабочих участка. Решение: Прежде чем вычислить
Для вычисления среднего стажа рабочих используем формулу средней арифметической взвешенной:
Средний стаж работы равен:
Средняя арифметическая взвешенная применяется для вычисления общей средней по групповым средним. Пример 4.6. По данным о числе вкладчиков и размере вклада за 1 квар-тал 2005 года по 3 филиалам Сбербанка района города (табл. 4.6), определить средний размер вклада (на 30.03.2005 г.).
Таблица 4.6. Число вкладчиков и размер вклада за 1 квартал 2005 г. по трем филиалам Сбербанка
Для определения среднего остатка вклада по трем филиалам в целом следует общую сумму остатков по вкладу для всех вкладчиков разделить на общее число вкладчиков.
где xi – среднее значение признака по каждой группе (в нашем случае – средний остаток по вкладу отдельного филиала); wi – веса средней (число вкладчиков по каждому филиалу);
Когда статистическая информация не содержит частот f по отдельным вариантам x совокупности, а представлена как их произведение Пример 4.7. Есть следующие данные о фонде зарплаты и средней зарплаты за ноябрь месяц по цехам предприятия (табл. 4.7.)
Таблица 4.7. Средняя зарплата и фонд заработной платы за ноябрь месяц по цехам предприятия
Определить среднюю месячную заработную плату работников предприятия. Решение: Условные обозначения следующие: w – фонд заработной платы по каждому цеху; х – средняя месячная заработная плата работников каждого цеха. Средняя заработная плата в ноябре исчислена по формуле средней взвешенной гармонической:
где Следовательно, средняя месячная заработная плата работников предприятия в ноябре 3483,7 руб. Пример 4.8.Автомобиль прошел первые 200 км со скоростью 75 км/ч, а оставшиеся 130 км со скоростью 85 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 330 км. Решение: Условные обозначения следующие:
Средняя скорость определяется как частное от деления всего пути (
Следовательно, средняя скорость автомобиля на протяжении всего пути была 78,65 км/ч. В том случае, если объемы явлений, т.е. произведения, по каждому признаку равны, применяется средняя гармоническая простая. Ее применяют при вычислении средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовление одного и того же вида продукции, одной и той же детали, изделия.
Пример 4.9.Две машины прошли один и тот же путь: одна со скоростью 70 км/ч, вторая – 85 км/ч. Определить среднюю скорость автомобилей. Решение: Средняя скорость исчисляется по формуле средней гармонической простой:
Следовательно, средняя скорость автомобилей 76,92 км/ч. Средняя квадратическаяприменяется для расчета среднего квадратического отклонения s, являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов). Средняя геометрическая(простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинаковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной (f – продолжительность периода, к которому относится средний коэффициент роста).
Пример 4.10. Выпуск продукции предприятия в течение четырех лет представлен в табл. 4.8.
Таблица 4.8. Выпуск продукции предприятием
Среднее значение коэффициента роста определяется по формуле средней геометрической:
Средний темп роста выпуска продукции за четыре года составил 116,7 %. 4.4. Структурные средние величины
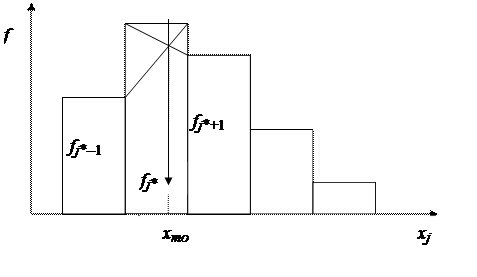
Структурные средние – мода и медиана – в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач. Модой называется значение признака, которое наиболее часто встречается в данном ряду распределения, т.е. имеет наибольшую частоту (частость). В дискретном ряду мода определяется визуально по максимальной частоте или частости. Моду и медиану можно определить на основе графического изображения ряда. Мода определяется по гистограмме распределения. Вначале отыскивается модальный интервал. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом следующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 4.1).
Рис. 4.1. Определение по графику значения моды
Моду можно определить и по формуле
где Медиана Для определения медианы сначала определяют ее место в ранжированном ряду, используя формулу
где п – число членов ряда. Если совокупность содержит четное число значений варьирующего признака (п = 2 k, k = n/2), то в этом случае за медиану условно принимают значение
так как в ряду нет члена, который делил бы совокупность на две равные по объему группы. В дискретном ряду распределения медиана определяется непосредственно по накопленной частоте, соответствующей номеру медианы. Пример 4.11.На кафедре работают 7 преподавателей. Требуется найти медиану (медианное значение) возраста преподавателей. Запишем в виде ряда номера преподавателей в порядке увеличения возраста (табл. 4.9).
Таблица 4.9. Распределение преподавателей по возрасту
Место медианы в ранжированном ряду определяем по формуле
Следовательно, медианный возраст преподавателей – 45 лет. В интервальном ряду распределения сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной. Приближенное значение медианы определяется по формуле
где Пример 4.12. Рассчитать моду и медиану по данным табл. 4.10.
Таблица 4.10. Распределение обуви, проданной коммерческой фирмой в январе 2002 г.
В этом ряду распределения мода равна 42. Именно этот размер обуви в январе 2002 г. пользовался наибольшим спросом. Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, ее половина – 50. Накопленная сумма частот ряда, впервые превышающая половину равна 62, ей соответствует значение признака, равное 40. Таким образом, 40-й размер обуви является медианным.
Контрольные вопросы для самопроверки
1. Что такое абсолютные статистические величины и каково их значение? Приведите примеры абсолютных величин. 2. В каких единицах измерения выражаются абсолютные статистические величины? Приведите примеры. 3. Что называется относительными величинами? 4. В какой форме могут быть выражены относительные величины? 5. Какие виды относительных величин вы знаете? Приведите примеры. 6. Дайте определение средней. 7. Какие виды средних величин применяются в статистике? Какие средние величины используются чаще всего? 8. Каковы основные свойства средней арифметической? 9. Для чего служит средняя гармоническая? Чем она отличается от средней арифметической? 10. Как исчисляется средняя геометрическая, где она применяется?
Поиск по сайту: |
 ) к фактической величине предшествующего периода (
) к фактической величине предшествующего периода ( 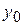 ), т.е.
), т.е. 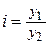 .
. = 1,057, или 105,7 %, т.е. инвестиции увеличились на 5,7 %.
= 1,057, или 105,7 %, т.е. инвестиции увеличились на 5,7 %. .
. .
. =
= 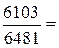 0,942 или 94,2 %.
0,942 или 94,2 %.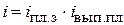 .
.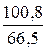 = 1,5. Это означает, что площадь Ростовской области больше в 1,5 раза, чем площадь Ставропольского края.
= 1,5. Это означает, что площадь Ростовской области больше в 1,5 раза, чем площадь Ставропольского края.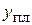 = 500×1,37 + 320×0,9 + 650×1,2 = 1753;
= 500×1,37 + 320×0,9 + 650×1,2 = 1753; = 520×1,37 + 300×0,9 + 690×1,2 = 1810,4.
= 520×1,37 + 300×0,9 + 690×1,2 = 1810,4. ×100% = 1810,4 / 1753 × 100 %= 103,27 %.
×100% = 1810,4 / 1753 × 100 %= 103,27 %.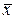 .
. 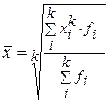 ,
,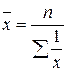
 ;
; 


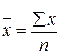



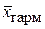 <
<  <
<  <
<  .
.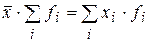 .
.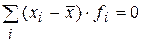 .
.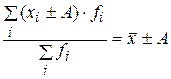 .
.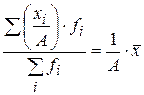 .
. .
.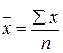 = (3000 + 3200 + 4000) / 3 = 3400.
= (3000 + 3200 + 4000) / 3 = 3400. . Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов:
. Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов: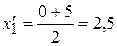 ;
; 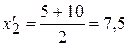 ;
; 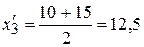 ;
; 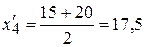 .
. .
.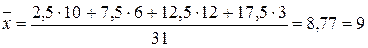 лет.
лет.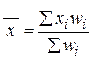 ,
,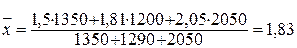 млн. руб.
млн. руб.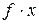 , применяется формула средней гармонической взвешенной.
, применяется формула средней гармонической взвешенной.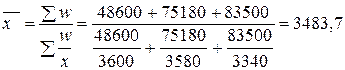 руб.,
руб.,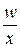 – численность работников каждого цеха за ноябрь.
– численность работников каждого цеха за ноябрь. – фонд заработной платы по каждому цеху;
– фонд заработной платы по каждому цеху;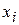 – средняя скорость автомобиля на отдельных участках пути;
– средняя скорость автомобиля на отдельных участках пути; – затраты времени на прохождения отдельных участков пути.
– затраты времени на прохождения отдельных участков пути.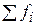 = 200 + 130) на общие затраты времени:
= 200 + 130) на общие затраты времени: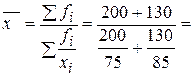
 км/ч.
км/ч.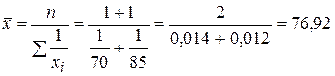 км/ч.
км/ч. .
.
 ,
, – левая граница модального интервала; b – величина модального интервала;
– левая граница модального интервала; b – величина модального интервала; 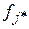 – частота модального интервала;
– частота модального интервала; 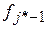 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; 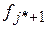 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным. – это значение признака, приходящееся на середину ранжированной совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части. При симметричном значении распределения статистической величины мода и медиана совпадают со средним значением этой величины:
– это значение признака, приходящееся на середину ранжированной совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части. При симметричном значении распределения статистической величины мода и медиана совпадают со средним значением этой величины:  .
.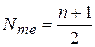 ,
,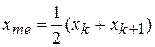 ,
, .
.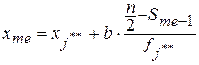 ,
, – нижняя граница медианного интервала;
– нижняя граница медианного интервала; 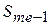 – накопленная частота интервала, предшествующего медианному,
– накопленная частота интервала, предшествующего медианному, 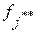 – частота медианного интервала.
– частота медианного интервала.