 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГЛАВА 5. ПОКАЗАТЕЛИ ВАРИАЦИИ ПРИЗНАКА
Показатели вариации
Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и квартильное отклонение. Размах колебаний,или размах вариации,представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности. Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции. Среднее линейное отклонение d и среднее квадратическое отклонение s показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения. Среднее линейное отклонение определяется по формулам: а) для невзвешенных данных (первичного ряда) б) для взвешенных данных: Среднее квадратическое отклонение s и дисперсия а) для несгрупированных данных
б) для сгрупированных данных
Формулу для расчета дисперсии можно преобразовать следующим образом: Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления: 1) дисперсия постоянной величины равна нулю; 2) если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится; 3) если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k2 раз. Квартильное отклонениеdk применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:
где Q3 и Q1 – соответственно третья и первая квартили распределения. Квартиль – значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три: первая квартиль (Q1), вторая квартиль (Q2), третья квартиль (Q3). Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы. Сначала определяют положение или место квартили:
Затем по накопленным частотам в дискретном ряду определяют численное значение. В интервальном ряду распределения сначала указывают интервал, в котором лежит квартиль, затем определяют ее численное значение по формуле где При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации.Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах. Формулы расчета относительных показателей вариации следующие: коэффициент осцилляции относительное линейное отклонение коэффициент вариации относительный показатель квартильной вариации Наиболее часто применяется коэффициент вариации.Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений близких к нормальному).
Моменты распределения Одна из задач анализа рядов распределения – выявление закономерностей распределения, определение его характера и количественного выражения. Кроме уже рассмотренных показателей, важной характеристикой рядов распределения являются моменты распределения. Момент распределенияMk – средняя арифметическая из отклонений значений признака xi от некоторой постоянной величины a в степени k. Порядок момента определяется значением k. Момент k-го порядка определяется как Mk = В зависимости от величины a различают начальные, центральные, условные моменты. Если a = 0, моментыназываются начальными и рассчитываются как Mk = При k = 0 получим начальный момент нулевого порядка, равный M0 = 1. При k = 1 получим начальный момент первого порядка, равный M1 = При k = 2 получим начальный момент второго порядка, равный M2 = Начальные моменты используются при расчете дисперсии: s2 = M2 – Если a = mk = mk = При k = 0 получим центральный момент нулевого порядка, равный m0 = 1. При k = 1 получим центральный момент первого порядка, равный m1 = 0. При k = 2 получим центральный момент второго порядка, равный m2 = s2 (дисперсии) и являющийся мерой вариации признака. Если постоянная величина равна a, моментыназываются условными и рассчитываются как mk =
Поиск по сайту: |
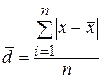 ;
;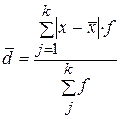 .
. определяются по формулам:
определяются по формулам: ;
; 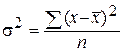 ;
; ;
;  .
. , т.е. дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической. При пользовании этой формулой исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от
, т.е. дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической. При пользовании этой формулой исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от 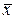 и исключается ошибка в расчете, связанная с округлением отклонений (
и исключается ошибка в расчете, связанная с округлением отклонений (  ).
). ,
, ;
;  ;
; 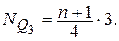
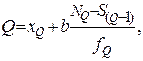
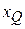 – нижняя граница интервала, в котором находится квартиль;
– нижняя граница интервала, в котором находится квартиль; 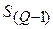 – накопленная частота интервала, предшествующего тому, в котором находится квартиль;
– накопленная частота интервала, предшествующего тому, в котором находится квартиль;  – частота интервала, в котором находится квартиль.
– частота интервала, в котором находится квартиль.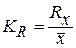 100 %,
100 %,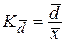 100 %,
100 %,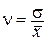 100 %,
100 %,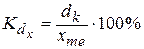 ,
, 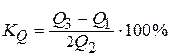 .
.
 .
. .
. .
. =
=  –
– 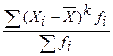 ;
;