 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Виды и схемы отбора единиц наблюдения в выборку
Доля выборки (в процентах) – отношение числа единиц выборки n к числу единиц генеральной совокупности N: Kв = (n / N) Так, при 2 % выборке (Kв = 0,02 = 2 %) из генеральной совокупности N = 2000 студентов объем выборки n составляет 40 человек, при 10 % выборке (Kв = 0,1 = 10 %) – n = 200 и т.д. Выборочная доля w или частность– отношение числа единиц выборки, обладающих данным признаком m, к общему числу единиц выборки n: w = m / n. Например, если из 100 студентов выборки (n = 100) 95 сдали сессию успешно (m = 95), то выборочная доля w = 95 / 100 = 0,95. Различают четыре вида отбора единиц наблюдения в выборку: случайный, механический, типический, серийный (гнездовой). Случайный отбор основан на принципе случайного выбора элементов из генеральной совокупности. Для этого всем элементам генеральной совокупности присваиваются свои номера, затем случайным образом производится отбор заданного количества элементов (например, тираж выигрышей в лото). Каждая единица наблюдения имеет одинаковую вероятность попадания в выборку, а количество отобранных единиц определяется исходя из принятой доли выборки. Механический отбор. Вся генеральная совокупность разбивается на равные группы по случайному признаку. Затем из каждой группы берется одна единица. Предварительно единицы генеральной совокупности располагают в определенном порядке (например, по алфавиту, местоположению, в порядке возрастания или убывания значений и т.д.), а потом, в зависимости от объема выборки, механически, через определенный интервал, отбирают необходимое количество единиц. При этом размер интервала (разность между максимальным и минимальным значениями) в генеральной совокупности равен обратному значению доли выборки (1 / Kв). Так, при 2 % выборке (Kв = 0,02) отбирается каждая 50-я единица (1 / 0,02 = 50), при 5 % выборке (Kв = 0,05) отбирается каждая 20-я единица (1 / 0,05 = 20), при 10 % выборке (Kв = 0,1) отбирается каждая 10-я единица (1 / 0,1 = 10), т.е. интервал зависит от объема выборки. Чем меньше выборка, тем больше интервал. При достаточно большой генеральной совокупности механический отбор по точности результатов близок к случайному отбору. Предыдущие виды отбора не учитывают особенности объекта, и поэтому выборки, полученные с их помощью, могут значительно отличаться по структуре от генеральной совокупности. Поэтому более представительными бывают выборки, отобранные с помощью типического отбора. Типический отбор. Генеральная совокупность разбивается на качественно однородные, однотипные группы по существенному, типическому признаку, влияющему на изучаемые показатели (например, при выборочном исследовании бюджетов населения выделяют прежде всего основные общественные группы: рабочие, крестьяне, служащие и пр.). Такие типические группы могут быть и не равными между собой по объему. Затем из каждой группы случайной или механической выборкой отбирается количество единиц, пропорциональное удельному весу группы во всей совокупности. Типический отбор дает более точные результаты, чем случайный или механический, так как при нем в выборку в такой же пропорции, как и в генеральной совокупности, попадают представители всех типических групп. Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Серийный (гнездовой) отбор. Отбору подлежат не отдельные единицы генеральной совокупности, а целые группы (серии, гнезда), отобранные случайным или механическим способом. В каждой такой группе проводится сплошное наблюдение, а результаты переносятся на всю совокупность. Точность серийной выборки зависит от того, насколько хорошо средние показатели группы будут представлять (репрезентировать) генеральную среднюю. Чем меньше серийные средние будут отклоняться от генеральной средней, тем точнее будут результаты выборки. По методу отбора различают повторную и бесповторную выборку. Повторный отбор – когда каждый отобранный элемент возвращается в генеральную совокупность и подлежит повторной выборке. Бесповторный отбор – когда элемент, попавший в выборку, не возвращается в генеральную совокупность. Комбинированный отбор – комбинация нескольких видов отбора; может проводиться в одну или несколько ступеней.
Ошибки выборки
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности. Теорема П.Л. Чебышева утверждает принципиальную возможность определения генеральной средней по данным случайной повторной выборки. Теорема Чебышева дополняется теоремой А.М. Ляпунова, которая позволяет рассчитать максимальную ошибку выборочной средней при данном достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней и ограниченной дисперсией вероятности того, что расхождение между выборочной и генеральной средней
где Величина
где D – предельная ошибка выборки; m – средняя ошибка выборки; t – коэффициент доверия, определяемый в зависимости от уровня вероятности. Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном отборесредняя ошибка определяется по формулам: 1) при повторном отборе: 2) при бесповторном отборе: где Можно определить предельные ошибки выборки и для доли признака. В этом случае дисперсия доли определяется по формуле
где Тогда при случайномотборе предельная ошибка 1) при повторном отборе: 2) при бесповторном отборе: Пределы доли признака в генеральной совокупности определяются следующим образом:
При расчете ошибок возникает существенное затруднение, так как величины s и p по генеральной совокупности неизвестны. Эти величины в условиях большой выборки заменяют величиной S (выборочная дисперсия) и w (выборочная доля), рассчитанными по выборочным данным. Формулы предельной ошибки позволяют решать задачи трех видов. 1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью). Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
где 2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину. Доверительная вероятность является функцией от t , определенной по формуле
По величине t определяется доверительная вероятность
Таблица 6.1. Значения вероятности для коэффициента доверия t
3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки. Объем выборки можно вычислить по следующим формулам. Случайная и механическая выборка: 1) повторная: 2) бесповторная: Покажем практическое применение рассмотренной выше методики на следующих примерах. Пример 6.1.[7]При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности. Решение. Для вероятности Рассчитаем предельную ошибку выборки:
Определим пределы генеральной средней: 30 – 0,84 < х < 30 + 0,84, или 29,16 < х< 30,84. Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 до 30,84 г. Пример 6.2. [7] С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью рабочих 480 человек была проведена 25 %-ная механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных рабочих потери рабочего времени составили более 45 минут в день. С вероятностью 0,683 установить пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 минут в день. Решение. Определяем объем выборочной совокупности: n =480 Выборочная доля w равна по условию 10 %. По табл. 6.1 определяем, что для вероятности
Пределы доли признака в генеральной совокупности: 10 – 2,4£ p £ 10 + 2,4, или 7,6£ p £ 12,4. Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями времени более 45 минут в день находится в пределах от 7,6 до 12,4 %. Ошибки и пределы генеральных характеристик при других способах формирования выборочной совокупности определяются на основе формул, отражающих особенности этих видов выборки. В случае типической выборки показателем вариации является средняя из внутригрупповых дисперсий Для типической выборки средняя ошибка вычисляется по формулам: 1) при отборе, пропорциональном объему типических групп:
2) при отборе, непропорциональном объему групп:
где Ni, ni – объемы i-й типической группы и выборки из нее соответственно; При серийной выборке средняя ошибка определяется следующим образом:
гдеr – число серий в выборочной совокупности; R – число серий генеральной совокупности; d2 – межгрупповая, межсерийная дисперсии;
Пример 6.3.[7] В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние урожайности по районам составили соответственно: 14,5; 16; 15,5; 15; 14 ц/га. С вероятностью 0,954 найти пределы урожайности во всей области:
Решение. Рассчитаем общую среднюю: Межгрупповая дисперсия:
Определяем предельную ошибку серийной бесповторной выборки (t = 2, P = 0,954):
Урожайность в области с вероятностью 0,954 будет находиться в пределах:
Следовательно, урожайность в области с вероятностью 0,954 будет находится в пределах от 13,3 до 16,7 ц/га. Объем выборки можно вычислить следующим образом.
1. Типическая выборка: повторный отбор – бесповторный отбор –
2. Серийная выборка: повторный отбор – бесповторный отбор – Пример 6.4. [7] В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала трех путевок, если по данным пробного обследования дисперсия составляет 225? Решение. По табл. 6.1 определяем для вероятности Рассчитаем необходимый объем выборки:
Следовательно, нужно обследовать 20 агентств, чтобы с вероятностью 0,683 ошибка не превышала трех путевок. Пример 6.5.[7]С целью определения доли сотрудников коммерческих банков в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников 12000 человек, в том числе 7000 мужчин, 5000 женщин. На основе предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определить необходимый объем выборки при вероятности 0,997 и ошибке 5 %. Решение. Рассчитаем общую численность типической выборки: Для вероятности
Вычислим объем отдельных типических групп: мужчины = женщины = Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в том числе 319 мужчин и 231 женщина.
Контрольные вопросы для самопроверки
1. В чем преимущества выборочного наблюдения перед сплошным? 2. Почему при выборочном наблюдении неизбежны ошибки и как они классифицируются? 3. Как производятся случайный, механический, типический и серийный отборы? 4. В чем различие повторной и бесповторной выборки? 5. По каким расчетным формулам находят средние ошибки выборки (для средней и доли) при повторном и бесповторных отборах? 6. Что характеризует предельная ошибка выборки и по каким формулам она исчисляется (для средней и доли)? 7. Что показывает коэффициент доверия? 8. Какими способами осуществляется распространение результатов выборочного наблюдения на всю совокупность? 9. Зачем и как исчисляются предельные статистические ошибки выборки (для средней и доли)? 10. По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью заданную точность наблюдения?
ГЛАВА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ
7.1. Виды связей между явлениями Все общественные явления взаимосвязаны между собой. Задача статистики выявить и измерить связи и зависимости между отдельными явлениями. Связь между явлениями классифицируется по ряду признаков, которые делятся на два класса: факторные, вызывающие измененияявлений, и результативные, изменяющиеся под влиянием факторных. Связи между явлениями и признаками классифицируются по степени тесноты, направлению, аналитическому выражению и количеству факторов, действующих на результативный признак. По первому критерию –степени тесноты связи выделяют функциональную и вероятностную (стохастическую) связь. Функциональная связь – связь, при которой определенному значению факторного признака соответствует только одно значение результативного признака. Особенностью такой связи является то, что в каждом отдельном случае известен полный перечень факторных признаков и точный механизм их влияния, выраженный определенным уравнением. Функциональные связи редко наблюдаются в социально-экономических процессах, чаще всего – в явлениях, описываемых точными науками. Примером функциональной связи в экономике может служить связь между оплатой труда и количеством изготовленных деталей при простой сдельной оплате труда. Вероятностная связь – связь, при которой причинная зависимость проявляется в общем, среднем при большом числе наблюдений. Особенностью вероятностной связи является то, что она проявляется во всей совокупности, причем не известен ни полный перечень факторных признаков, ни точный механизм их влияния на результативный признак. В социально-экономической жизни такие связи встречаются часто. Существуют количественные критерии оценки тесноты связи, которые будут рассмотрены ниже. Для изучения функциональных связей применяются балансовый и индексный методы. Для исследования вероятностных связей используются метод сопоставления двух параллельных рядов, метод аналитических группировок, корреляционный и регрессионный анализ. По второму критерию –по направлению выделяют прямую и обратную связь. При прямой связи направление изменения результативного признака совпадает с направлением изменения признака-фактора, т.е. с увеличением факторного признака увеличивается и результативный, и наоборот, с уменьшением факторного признака уменьшается и результативный признак. В противном случае между рассматриваемыми величинами существуют обратные связи. По третьему критерию – аналитическому выражениювыделяют линейные и нелинейные связи. При линейной связи с возрастанием значения факторного признака происходит непрерывное возрастание или убывание значений результативного признака. Математически такая связь представляется уравнением прямой, а графически – прямой линией. При нелинейных связях с возрастанием значения факторного признака возрастание или убывание результативного признака происходит неравномерно или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.). По последнему критерию – количеству факторов, действующих на результативный признак, выделяют однофакторные и многофакторные связи. Однофакторные (простые) связи обычно называют парными (так как рассматривается пара признаков). В случае многофакторной (множественной) связи все факторы действуют комплексно, т.е. одновременно и во взаимосвязи. Рассмотрим методы изучения взаимосвязей между явлениям. В методе сопоставления двух параллельных рядов значения факторного признака располагают в возрастающем или убывающем порядке, а затем прослеживают направление изменения величины результативного признака. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяет нам установить наличие связи и ее направление. До того как применять этот метод, необходимо провести анализ сопоставляемых явлений и установить наличие между ними причинных связей (а не простого сопутствия). К недостаткам этого метода следует отнести невозможность определения количественной меры связи между изучаемыми признаками. Чтобы выявить зависимость с помощью метода аналитических группировок, нужно провести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Сопоставляя затем изменения результативного признака по мере изменения факторного признака, можно выяснить направление, характер и тесноту связи между ними. Однако с помощью этого метода нельзя определить форму (нельзя подобрать аналитическое выражение) влияния факторных признаков на результативный признак Корреляционный и регрессионный анализ играют наиболее важную роль при исследовании связей между признаками. Поэтому рассмотрим их применение более подробно.
7.2. Корреляционный и регрессионный анализ
Задачи корреляционного анализа сводятся к следующему: - измерение тесноты связи между варьирующими признаками; - определение неизвестных причинных связей; - оценка факторов, оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа есть: - выбор типа модели (формы) связи; - установление степени влияния независимых переменных на зависимую переменную (функцию регрессии); - определение расчетных значений зависимой переменной. Решение всех перечисленных задач приводит к необходимости комплексного использования корреляционного и регрессионного анализа. Статистическое моделирование связи между явлениями общественной жизни при этом состоит из следующих этапов. 1.Отбор факторных признаков для включения их в модель связи. В его основе лежит качественный и логический анализ явления, связанный с изучением его природы методами экономики, социологии. 2.Выбор типа модели связи (уравнения регрессии). Он может опираться на теоретические знания об изучаемом явлении, на опыт предыдущих аналогичных исследований или на анализ графического изображения статистических данных. Другим способом выбора уравнения регрессии является метод перебора различных уравнений с последующей статистической проверкой на основе t-критерия Стьюдента и F-критерия Фишера. Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь должен стремиться к увеличению числа наблюдений, так как большой объем наблюдений обеспечивает адекватность статистических моделей. Адекватность модели – соответствие теоретических величин фактическим статистическим данным. 3. Построение модели связи, т.е. определение неизвестных параметров множественной регрессии
Для определения минимума данной функции приравнивают к нулю её частные производные и получают систему нормальных уравнений для нахождения Так, для расчета параметров линейной двухфакторной регрессии
система нормальных уравнений будет иметь вид:
Параметры системы могут быть найдены методами численного моделирования (например, методом Гаусса) или с помощью прикладных программ (Eureka, MathCad, Excel и др.). 4.Оценка существенности корреляции. Для этого рассчитывают разного рода характеристики тесноты связи между зависимой и независимой переменными: парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации. 5. Проверка адекватности полученной модели связи, которая заключается в оценке значимости коэффициентов регрессии и уравнения регрессии. Она осуществляется на основе t-критерия Стьюдента и F-критерия Фишера. 6. Экономическая интерпретация коэффициентов уравнения регрессии. Она вновь связана с качественными особенностями изучаемого явления. При этом вычисляются частные коэффициенты эластичности, β-коэффициенты.
Поиск по сайту: |
 %.
%. не превзойдет по абсолютной величине некоторую величину
не превзойдет по абсолютной величине некоторую величину  , равную интегралу Лапласа. Это можно записать следующим образом:
, равную интегралу Лапласа. Это можно записать следующим образом: ;
;
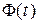 – интеграл Лапласа (нормированная функция Лапласа).
– интеграл Лапласа (нормированная функция Лапласа).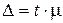 ,
, ;
; ,
, – выборочная (или генеральная) дисперсия; s – выборочное (или генеральное) среднее квадратическое отклонение; n – объем выборочной совокупности; N – объем генеральной совокупности.
– выборочная (или генеральная) дисперсия; s – выборочное (или генеральное) среднее квадратическое отклонение; n – объем выборочной совокупности; N – объем генеральной совокупности.
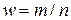 – доля единиц, обладающих данным признаком в выборочной совокупности.
– доля единиц, обладающих данным признаком в выборочной совокупности.  может вычисляться по формуле:
может вычисляться по формуле: ;
; .
. .
. ;
; ,
,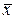 и
и 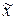 – генеральная и выборочная среднее соответственно; D – предельная ошибка выборочной средней.
– генеральная и выборочная среднее соответственно; D – предельная ошибка выборочной средней. .
. ;
; .
. = 4.
= 4. =
=  = 3 4/
= 3 4/  = 0,84.
= 0,84. = 120 человек.
= 120 человек.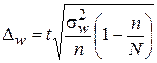 =
=  или2,4 %.
или2,4 %. , при серийной выборке – межгрупповая дисперсия
, при серийной выборке – межгрупповая дисперсия  .
. – повторный отбор;
– повторный отбор; – бесповторный отбор;
– бесповторный отбор;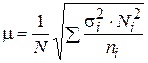 – повторный отбор;
– повторный отбор; – бесповторный отбор,
– бесповторный отбор, – групповые дисперсии.
– групповые дисперсии. – повторный отбор;
– повторный отбор; – бесповторный отбор,
– бесповторный отбор, .
.
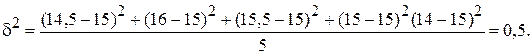
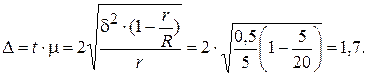

 ;
;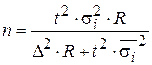 .
. ;
;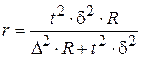 .
. =
= 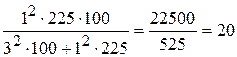 .
. чел.
чел. человек;
человек; человек.
человек. ,
,  ,...,
,...,  . Неизвестные определяются по методу наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений эмпирических данных
. Неизвестные определяются по методу наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений эмпирических данных  от выравненных
от выравненных 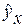 :
: .
.
