 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы анализа тенденции развития в рядах динамики
Одна из задач статистики – определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие других факторов может носить случайный характер. Поэтому при анализе динамики исследоваться должна основная тенденция, устойчивая на протяжении изучаемого этапа развития. Основная тенденция развития (тренд) –плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. С целью выявления тренда ряды динамики исследуются методами укрупнения интервалов, скользящей средней и аналитического выравнивания. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции, который, в свою очередь, может быть заменен рядом квартального выпуска продукции. Сравнение средних, вычисленных по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, но не математическую модель тренда. Метод скользящей средней основан на расчете средней величины, которая вычисляется по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа членов, начиная со второго:
Таким образом, средняя как бы «скользит» по ряду динамики. Если в ряду динамики имеются периодические колебания, то период скользящей средней совпадает с периодом колебания или будет кратным ему. Метод позволяет выявить направление и характер основной тенденции развития, но не математическую модель тренда. Метод аналитического выравниванияпозволяет определить аналитическое выражение, отражающее закономерность изменения явления как функцию времени yt = f(t). Метод основан на замене фактических значений уровней yi плавно изменяющимися величинами yt. Выбор типа модели может основываться на анализе графического изображения уровней динамического ряда. Выравнивание по прямой линии используется, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии. Выравнивание по показательной функции используется, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Расчет параметров функции f(t) производится методом наименьших квадратов. Когда тип тренда установлен, вычисляют оптимальные значения параметров тренда, исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). В этом методе минимизируется сумма квадратов отклонений фактических уровней динамического ряда Если количество уровней в ряду динамики нечетное, то временные даты (t) обозначаются следующим образом (табл. 8.3):
Таблица 8.3. Представление показателя времени
Если количество уровней в ряду динамики четное, то счет ведется полугодиями и обозначения временных дат (t) принимают следующий вид (табл. 8.4): Таблица 8.4. Представление показателя времени
При выборе формы уравнения тренда следует учитывать объем имеющийся информации. Чем больше параметров в уравнении тренда, тем больше требуется уровней ряда динамики для одной и той же степени надежности. Выбор формы уравнения тренда может осуществляться и на основе формального критерия. Основная тенденция развития в рядах динамики с постоянными абсолютными приростами отображается линейным уравнением
где
где yt – исходные уровни ряда динамики; n – число членов ряда; t – показатель времени. Решение системы дает следующее выражение для
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этой цели показателем времени придают такие значения, чтобы их сумма была равна нулю, т.е.
откуда Пример 8.4. [14] Определить уравнение тренда по данным, представленным в табл. 8.5
Таблица 8.5. Динамика затрат на производство с 1999 по 2003 г.
По итоговым данным нашего примера (см. табл. 8.5) получим:
уравнение основной тенденции за 1999–2003 годы
Подставляя в уравнение принятые значения t, получим: 1999 год – 2000 год –
Поиск по сайту: |
 ,
,  ,
, 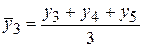 и т.д.
и т.д. от выровненных уровней
от выровненных уровней  (от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую, рассчитывают параметры тренда. Однако вычислительный процесс определения параметров тренда при сохранении полной идентичности конечных результатов может быть упрощен, если ввести обозначения дат (периодов) таким образом, чтобы
(от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую, рассчитывают параметры тренда. Однако вычислительный процесс определения параметров тренда при сохранении полной идентичности конечных результатов может быть упрощен, если ввести обозначения дат (периодов) таким образом, чтобы  .
.





 ,
, ,
,  – неизвестные параметры, для расчета которых по способу наименьших квадратов необходимо решить систему нормальных уравнений
– неизвестные параметры, для расчета которых по способу наименьших квадратов необходимо решить систему нормальных уравнений

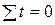 (см. табл. 8.3, 8.4). При этом уравнения примут вид
(см. табл. 8.3, 8.4). При этом уравнения примут вид
 представляет собой средний уровень динамики ряда
представляет собой средний уровень динамики ряда 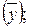 параметр
параметр  является коэффициентом регрессии, определяющим направление и темпы развития. Если
является коэффициентом регрессии, определяющим направление и темпы развития. Если  , то уровни выровненного ряда динамики равномерно возрастает, а при
, то уровни выровненного ряда динамики равномерно возрастает, а при 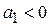 происходит равномерное снижение.
происходит равномерное снижение.
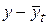


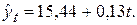
 ,
, и т. д.
и т. д.