 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решений на основе уравнения регрессии
Проверка адекватности модели, построенной на основе уравнения регрессии, начинается с проверки значимости каждого коэффициента регрессии. Оценка значимости коэффициентов регрессии осуществляется с помощью t-критерия Стьюдента при n – k – 1 степенях свободы. Отметим, что t-критерий Стьюдента – это коэффициент доверия по распределению Стьюдента При линейной зависимости y от
где n – число наблюдений; k – число факторных признаков в уравнении регрессии; ν = n – k – 1 – число степеней свободы, характеризует число свободно варьирующих элементов совокупности. Параметр модели признается статистически значимым, если
Величины Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа. Оценку значимости коэффициентов регрессии с помощью t-критерия используют для завершения отбора существенных факторов в процессе многошагового регрессионного анализа. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов. Проверка значимости уравнения регрессии производится на основе вычисления F-критерия Фишера:
где Полученное значение – критерий Fрасч сравнивают с критическим (табличным) для принятого уровня значимости a и чисел степеней свободы Это означает, что доля вариации, обусловленная регрессией, намного превышает случайную ошибку. Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если Fрасч превышает табличное не менее чем в 4 раза.
Поиск по сайту: |
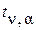 при уровне значимости случайностей a (a = 1 – Ф(t). В социально-экономических исследованиях значение a обычно принимается равным 0,05 (т.е. доверительная вероятность Ф(t) = 0,95 или 95 %).
при уровне значимости случайностей a (a = 1 – Ф(t). В социально-экономических исследованиях значение a обычно принимается равным 0,05 (т.е. доверительная вероятность Ф(t) = 0,95 или 95 %).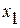 и
и  (двух факторов) формулы для расчета t-критерия имеют вид:
(двух факторов) формулы для расчета t-критерия имеют вид: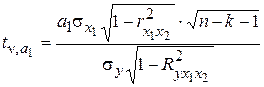 ;
;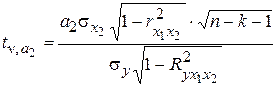 ,
, .
.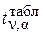 при различных значениях n и уровнях значимости a приведены в [4, 5, 7, 16].
при различных значениях n и уровнях значимости a приведены в [4, 5, 7, 16]. ,
,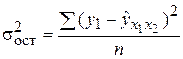 – остаточная дисперсия.
– остаточная дисперсия.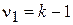 и
и  . Величины Fтабл при различных значениях
. Величины Fтабл при различных значениях 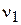 ,
,