 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оценка существенности корреляции
Измерение тесноты и направления связи – важная задача изучения и количественной оценки взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного или нескольких факторов. Оценка существенности корреляции признаков предполагает расчет и анализ следующих величин: парных, частных и множественных коэффициентов корреляции, множественного коэффициента детерминации. Подчеркнем, что перечисленные параметры определяются только для линейной связи между признаками. Значения коэффициента корреляции находятся в пределах –1 £ r £ +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Интерпретация значений r по характеру связи и степени тесноты связи дана в табл. 7.1,7.2. Таблица 7.1. Оценка линейного коэффициента корреляции r по степени тесноты связи
Таблица 7.2. Оценка линейного коэффициента корреляции r по характеру связи
В теории разработаны и на практике применяются различные модификации формул для расчета парных коэффициентов корреляции. Ниже приведены наиболее простые формулы для случая двухфакторной линейной модели. Для более сложной формы связи формулы получают по аналогии.
Средние квадратические отклонения вычисляются как:
Проверка адекватности модели связи. Принятие
Поиск по сайту: |
 ;
;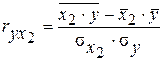 ;
; .
.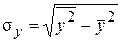 ;
;  ;
; 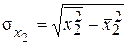 .
.