 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамическая идентификация
В предыдущих разделах были рассмотрены экспериментальные методы получения статических моделей одномерных и многомерных объектов. Но более важными с точки зрения работы системы автоматизации являются динамические характеристики. Динамические характеристики объектов управления можно получать аналитически в виде дифференциальных уравнений некоторого порядка. Применяя разработанные математиками методы анализа, изучаемые в курсе ТАУ, можно анализировать работу объекта управления, не решая дифференциальных уравнений. Но все равно нужно иметь аналитическую модель объекта или модели его составных частей. Чем сложнее объект, тем сложнее модель, тем труднее ее вывести аналитически. Экспериментальные методы позволяют получить формальную модель практически любого объекта. При этом порядок получения динамической модели аналогичен получению статической модели, основные этапы те же. Но есть и отличия. Так пассивный эксперимент выполняется также в эксплуатационных переходных режимах, при изменении во времени управляющих и возмущающих воздействий. Активный эксперимент основан на задании объекту специально сформированных управляющих или возмущающих воздействий типа гармонических, скачкообразных или импульсных воздействий. Уравнение регрессии при экспериментальном получении динамической модели объекта управления уже не алгебраическое и не дифференциальное, а разностное. Разностное уравнение – это форма представления дифференциального уравнения при численном его решении, изучается в одном из разделов высшей математики (численные методы и конечные разности). Для дифференциального линейного уравнения порядка l аналогом будет разностное уравнение вида
где k – номер эксперимента; А и В – коэффициенты разностного уравнения. Поскольку порядок идентифицируемого объекта обычно не известен, то начинают его идентификацию с самой простой модели – разностного уравнения первого порядка:
Если модель оказывается не достаточно адекватной, берут разностное уравнение второго порядка и так далее. Для определения коэффициентов А и В разностного уравнения используется та же методика минимизации суммы квадратов отклонений:
где N – число экспериментальных точек. Система уравнений типа частных производных имеет вид
Так как в динамике модель объекта управления описывается дифференциальным уравнением, то и в результате обработки экспериментальных данных получают дифференциальное уравнение, коэффициенты передачи k и постоянные времени Т которого определяются по полученным коэффициентам разностного уравнения А и В. Проверка адекватности модели объекту выполняется путем сравнения расчетных значений параметров объекта согласно полученной модели с экспериментальными данными. Таким образом, были рассмотрены простейшие случаи получения экспериментальным путем гладких, устойчиво без разбросов повторяющихся моделей объектов управления, пригодность которых оценивается по допустимому максимальному отклонению от эксперимента. На практике встречаются объекты, у которых при опытах с одними и теми же значениями входных параметров получаются неповторяющиеся значения выходных параметров. Такие объекты называются недетерминированными и требуют иного подхода при изучении.
Поиск по сайту: |
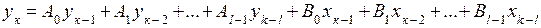 , (3.11)
, (3.11)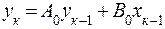 .
.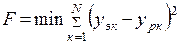 ,
,
 …;
…; 
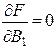 ; …
; …