 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Количественная оценка информации
В асу тп информация (сообщения) передается в основном в закодированном виде. Для количественной оценки передаваемой кодированной информации введены понятия количества информации и энтропии. Считается, что если поступление некоторого сообщения имеет большую вероятность, то такое сообщение несет мало информации, и, наоборот, если сообщение неожиданно, то в нем содержится много информации. Но это так же субъективная оценка. У нас есть конкретная формула количества возможных сообщений (2.1). С увеличением m и n увеличивается и количество сообщений N. С увеличением основания m и числа разрядов n, очевидно, увеличивается степень новизны каждого сообщения и, следовательно, количество информации в каждом из сообщений. Р.Хартли предложил способ определения количества информации, приходящееся на одно сообщение, по логарифму числа возможных сообщений при данном способе кодирования:
Здесь а – основание логарифма. Т.к. для кодирования в основном применяется двоичная система, то а чаще всего равно 2. Тогда при m = 2 и n = 1 получим единицу измерения количества информации. Если а не 2, а 10 ,то получаем десятичную единицу измерения информации. Формула (2.3) справедлива только в том случае, если вероятность появления отдельных символов в сообщении одинакова: при m = 2: Р0 = 0,5 и Р1 = 0,5; при m = 10: Р0 = 0,1, Р1 = 0,1, … Р9 = 0,1. При этом вероятность появления любого из сообщений р = 1 / N (2.4) и тогда Количество информации в сообщении зависит от вероятности появления сообщения (чем больше вероятность, тем меньше I, как и записали ранее). Если равновероятность не соблюдается, то требуется другой способ определения I. Возьмем самый сложный случай сообщения, алфавит которого состоит: из m символов b1 ,b2,.......,bm; вероятность появления этих символов в сообщении р1, р2,...,рm; количество разрядов n. Поэтому каждый из символов bi может появиться в сообщении несколько раз. Вероятность появления любого из сообщений равна произведению вероятностей появления каждого из символов:
Здесь li – число раз появления bi -го сообщения, Σ li= n; Pi – вероятность появления символа bi. При значительном числе разрядов n Pi=li / n, li=nPi или
Теперь, используя формулу (2.5), получаем количество информации:
формула шеннона. Если снова предположить р1= р 2=....= р m=1/m, то после подстановки в формулу (2.6) получим ту же формулу (2.3). Количество информации, приходящееся на 1 разряд сообщения, называется энтропией:
так же формула шеннона. Энтропия характеризует степень неопределенности появления сообщений. Для того же самого сообщения, если р1=1, а все остальные сообщения р = 0, то
Энтропия минимальна, т.е. никакой неопределенности. Все сообщения во всех разрядах имеют элемент b1. Информации тоже никакой I = 0. Для того же сообщения, если р1 = р 2 =....= р m = 1 / m, то
Неопределенность максимальная, т.к. в каждом разряде может стоять любой из элементов bi. При m = 2 и а = 2 Н = 1 и пределы изменения Н: 0 ≤ Н ≤ loga m. (2.9) Понятия I и H в телемеханике некоторыми авторами используются для оценки появления целого сообщения, т.е. I = N, H = n loga m, бит/сообщение. В АСУ ТП понятия Н и I используются еще и для оценки упорядоченности технологического объекта и определения необходимого объема управления. Там формула энтропии записывается как
где R – количество возможных результатов управления. Если а = 2, то Н измеряется в битах. Если а = 10, то Н измеряется в десятичных единицах энтропии: Rmin = 1, Rmax = ∞. Очевидно, R всегда < ∞, и цель управления – получить R = 1. Если все результаты равновероятны, то вероятность появления каждого из них: P = 1 / R, значит
совпадает с формулой (2.5) для I в телемеханике. В действительности результаты управления неравновероятны и энтропия НТО должна определяться с учетом вероятности появления отдельных результатов Pi, т.е. определяется усредненная величина НТО. В теории вероятности эта усредненная величина называется математическим ожиданием, она равна сумме произведений случайной величины (Нi – энтропии отдельных результатов) на вероятность появления этой случайной величины (Pi):
формула Шеннона, такая же, как формула (2.7) в телемеханике. Повышение упорядоченности ТО, на которое направлено применение АСУ ТП, ведет к снижению количества возможных результатов управления, т.е. к снижению Н. В телемеханике Н должно быть как можно больше, а в АСУ ТП – как можно меньше: Нкон < Ннач, где Ннач – без АСУ ТП, Нкон – с АСУ ТП. Разность Ннач – Нкон = I (2.13) называется в автоматике необходимым объемом управления или информацией. Это также несколько отличается от определения информации в телемеханике. Если же распишем уравнение (2.13) подробнее, то получим:
или
Если Rкон = 1, то и Ркон = 1, тогда
Необходимый объем управления совпадает с формулой (2.5) для I в телемеханике. Та же единица измерения, но смысл немного другой. Таким образом, для аппаратной реализации наиболее удобно представление количества информации в равномерном коде. При одинаковой или примерно одинаковой вероятности появления символов b1 … bm. I определяется в основном количеством разрядов – n, то есть по n можно сравнивать различные средства телемеханики. Так как вероятность появления символов b1 … bm все же неодинакова, то для оценки I в различных системах служит энтропия Н (бит/символ) – степень неопределенности появившегося сообщения. В АСУ ТП Н должна быть как можно меньше, т.е. Н → 0. При нескольких результатах управления и неодинаковой вероятности результатов Н > 0 и определяется математическим ожиданием М энтропии:
Информация в АСУ ТП называется необходимым объемом управления и в пределе совпадает с формулой I для ТМ:
Поиск по сайту: |
 . (2.3)
. (2.3) – одна двоичная единица – 1 бит.
– одна двоичная единица – 1 бит. . (2.5)
. (2.5) .
.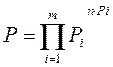 .
. ,
,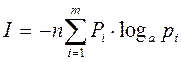 , (2.6)
, (2.6) , (2.7)
, (2.7) .
. ,
, . (2.8)
. (2.8) , (2.10)
, (2.10) (2.11)
(2.11) , (2.12)
, (2.12)
 .
. . (2.14)
. (2.14) .
. .
.