 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Идентификация одномерных детерминированных объектов
Для одномерных объектов при отсутствии случайных помех наиболее подходит модель в виде степенного полинома
хотя могут быть и другие модели. Степень полинома ориентировочно определяется по разности ординат экспериментально полученной зависимости у = ƒ(х) и при постоянных приращениях аргумента ∆х = const. При неизменных разностях между ординатами модель описывается полиномом первой степени:
При неизменных разностях между разностями второго порядка – полиномом второй степени и т. д.:
Оптимальной считается модель, у которой при полученных в результате эксперимента коэффициентах ai и степени n минимальна сумма квадратов отклонений расчетных значений ур от экспериментальных значений уэ. Записывается в виде
или
где N – число опытов. Коэффициенты модели определяются из системы уравнений типа частных производных:
Для упрощения расчетов по системе (3.8), во – первых, за начало отсчета аргумента принимается середина интервала экспериментальных данных xК (x1, xК xN). Во – вторых, отсчет аргумента ведут в относительных единицах и для расчета берут симметричные значения xК (0, – 1,+1, – 2,+2 и т. д.). В этом случае все суммы нечетных степеней функционала (3.7) равны нулю, упрощается система (3.8), упрощается расчет коэффициентов. При этом у также можно брать в относительных единицах. Например, имеем модель
Получены экспериментальные значения у и х. Требуется определить коэффициенты а0, а1, а2. Записываем функционал (3.7) для экспериментальных данных
и находим его частные производные по неизвестным коэффициентам:
Так как суммы нечетных степеней х равны нулю по условию эксперимента, то рассматриваем скобки и получаем систему:
При этом произведение уэк × хэк2 не сокращается, так как уэк в симметричных точках хэк может быть различно. Решение системы относительно коэффициентов а0, а1, а2 имеет вид
Модель получена (определена). На практике бывают и другие полиномы с отрицательными и дробными степенями, например, у = а0 + а1 х +а2 х – 1. Обобщенная модель степенного полинома:
где n – количество членов номинала – целое число; mi – целое или дробное число любого знака. Если при равных приращениях хэ величина уэ растет примерно в геометрической прогрессии, то применяют модели вида
Такая же модель у = авх получается, если для хэ и уэ наблюдается линейная зависимость между хэ и lg уэ, т.к. из уравнения модели имеем lg уэ = lg a + хэ lg в. Во всех случаях критерием оптимальности модели служит минимум суммы квадратов отклонений.
Поиск по сайту: |
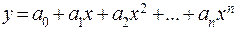 , (3.6)
, (3.6) .
. .
. (3.7)
(3.7) ,
, . (3.8)
. (3.8) .
.
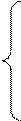
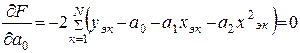 ,
, ,
, .
.
 ,
,  .
. ,
,  ,
, 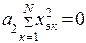 .
.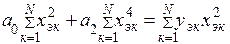 .
.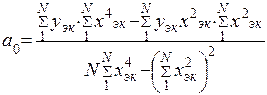 ,
,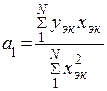 ,
,  .
. , (3.9)
, (3.9)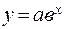 или
или  .
.