 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Синтез комбинационных автоматов
Для создания сложных комбинационных автоматов используются элементарные комбинационные автоматы – логические элементы. С их помощью реализуются логические функции, связывающие входные и выходные переменные в каждом такте работы комбинационного автомата: y1i=f1(x1i,x2i....xni); ................................. (4.5) ymi=fm(x1i,x2i....xni) их называют еще переключательными функциями. Синтез комбинационного автомата начинается с содержательного описания функционирования объекта и составления таблицы истинности. Для получения аналитического выражения, определяющего необходимую структуру автомата (4.5), по таблице истинности записываются исходные формы переключательных функций в виде совершенной дизъюнктивной (СДНФ) или конъюнктивной (СКНФ) нормальной формы, которые затем минимизируются с помощью основных законов алгебры логики. СДНФ представляет собой дизъюнкцию (сумму) минтермов, а СКНФ – конъюнкцию (произведение) макстермов. Минтермом или конституэнтой единицы называется логическая функция, принимающая значение ''1'' только на одном наборе входных переменных. Образуется как конъюнкция всех входных переменных с отрицанием тех, которые в данном наборе равны нулю. Число минтермов равно числу наборов, в которых выходная величина равна "1". Макстермом или конституэнтой нуля называется логическая функция, принимающая значение ''0'' только на одном наборе переменных. Образуется как дизъюнкция входных переменных, где переменные данного набора, равные единице, взяты с отрицанием. Число макстермов равно числу наборов, в которых выходная величина равна ''0''. Две эти формы эквивалентны. Но при минимизации удобно пользоваться СДНФ. Рассмотрим это на простейшем примере. Есть таблица истинности логических элементов – "исключающее ИЛИ":
СДНФ ― В том, что они эквивалентны, убедимся, раскрыв скобки во второй записи:
От таблицы истинности остается только половина возможных ПФ. Как проводится минимизация. Во-первых, к полученной СДНФ применяется закон склеивания, отыскиваются смежные минтермы (минтермы, отличающиеся значением только одного аргумента). Склеиваясь по этому аргументу, смежные минтермы образуют импликанты – конъюнкции с числом сомножителей, меньшим на единицу. Импликанты, в свою очередь, могут склеиваться между собой. Несклеивающиеся импликанты называются простыми. Например, в описании (в СДНФ) какого-то устройства есть такие минтермы
Смежными будут минтермы 1 и 2, а также 2 и 3, они склеиваются попарно. В результате остаются две смежные импликанты, которые, склеиваясь, дают простую импликанту. Закон склеивания
Во вторых, сокращенную после склеивания СДНФ приводят к тупиковой форме следующим способом: 1. Устраняют избыточные импликанты. При этом применяют закон тавтологии. Если при склеивании получились одинаковые импликанты, то оставляют одну из них (закон тавтологии х + х = х). 2. Применяют закон поглощения для простых импликант и оставшихся минтермов и более длинных импликант. Например, 3. Проводят испытания отдельных членов ПФ. Для этого отбрасывается одно из слагаемых, а в оставшиеся выражения подставляются значения аргументов, обращающие испытываемое слагаемое в единицу. Если оставшаяся часть при этом тождественно равна 1, то испытываемое слагаемое лишнее, если "0", то не лишнее. Например, в полученном выражении исключающего ИЛИ
отбросим второе слагаемое
значит х1 = 0 и Этот метод называется методом Квайна и применим для числа аргументов до 5 – 6. При большем числе аргументов применяют машинные методы минимизации (например, метод Мак-Класки). Большое распространение также получил метод минимизации с помощью карт Карно (метод Вейга-Карно). Смысл его заключается в том, что по табличной записи СДНФ проводится графическое склеивание. Так получается запись уравнения ПФ автомата для составления его схемы из логических элементов И, ИЛИ, НЕ. Для перехода к многофункциональным базисам Шеффера (И-НЕ) или Пирса (ИЛИ-НЕ) применяется закон Моргана – Шеннона. В первом случае берется двойное отрицание всего выражения тупиковой формы СДНФ. Во втором – двойное отрицание каждого слагаемого и всего выражения СДНФ. Например, имеем тупиковую форму СДНФ аппарата
тогда
Поиск по сайту: |
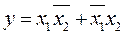 ; СКНФ –
; СКНФ –  .
. .
. .
. :
: – простая импликанта.
– простая импликанта. (закон поглощения
(закон поглощения 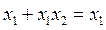 ).
).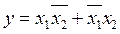 ,
,
 ,
,  ,
,  ,
,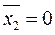 , теперь
, теперь  , т.е. испытываемое слагаемое не лишнее.
, т.е. испытываемое слагаемое не лишнее. ,
, .
.