 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Преобразование технологической информации
Сигналы внешней априорной информации (рис.1.1), представляющие собой сведения о целях и задачах управления, в процессе работы АСУ ТП специальных преобразований не требуют. Преобразованию подлежит текущая информация, при этом выделяют 2 аспекта преобразования: – преобразование природы, формы и параметров сигналов; – установление однозначного соответствия между отдельными сигналами. Преобразование природы и формы сигналов рассматривались в курсах ТСА, ТОЭ, ТАУ, «Электрические измерения» и др. Необходимость установления однозначного соответствия между отдельными видами сигналов возникает при передаче сложных несинусоидальных сигналов между пунктами передачи и приема информации. Основные виды сложных сигналов представлены на рис. 2.2.
а) б) в) г) рис. 2.2. Основные виды сложных сигналов: а – прямоугольный; б – треугольный; в – пилообразный; г – непериодический
Основные виды преобразований: модуляция; разложение; квантование; кодирование. Разложение сигналов
Сложный периодический сигнал прямоугольной, треугольной, пилообразной формы разлагается на составляющие гармоники с помощью преобразований Фурье. Для передачи таких сигналов с некоторой точностью достаточно передавать постоянную составляющую и несколько гармоник. Непериодический сигнал также с помощью преобразований Фурье может быть представлен бесконечной суммой гармонических составляющих с комплексными амплитудами. Для передачи этих сигналов с заданной точностью требуется определенный спектр частот гармонических составляющих. Ввиду большой сложности таких преобразований обычно применяют другие методы. Квантование сигналов
Для непосредственной, без разложения на составляющие, передачи непрерывных периодических и непериодических функций выполняется, во-первых, разбиение или квантование их по времени с некоторым шагом ∆t, то есть значения функций передают только в моменты времени t1, t2,..(рис 2.3). Чем меньше ∆t, тем точнее передача.
U(t)
t1 t2 t3 t4 t5 t6 t, с рис. 2.3. Квантование сложных сигналов по времени Частота квантования определяется на основании теоремы В.А. Котельникова: если непрерывная функция U(t) имеет ограниченный частотный спектр (его можно ограничить с помощью преобразований Фурье), то она полностью определяется своими мгновенным значениями, отсчитанными через интервалы времени:
где Fс – ширина спектра частот функции U(t).
U, в
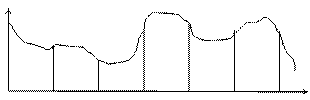
2 4 6 t, с Рис.2.4. График функции произвольного сигнала Чтобы передавать ограниченное количество значений U(t), выполняется также квантование U(t) по амплитуде (уровню), рис. 2.4. Весь диапазон изменения U(t) Umax – Umin разбивается на m уровней с некоторым шагом ∆U:
Для данного графика имеем 7 уровней по напряжению. Но теперь передача будет выполняться с ошибкой – абсолютной погрешностью:
Относительная погрешность:
При Чем больше уровней, тем меньше погрешность. Шаг квантования (количество уровней) выбирается, исходя из допустимой погрешности и в зависимости от величины помех в канале связи. Модуляция
В телемеханических системах для передачи сообщений от передатчика к приемнику используют промежуточные сигналы-переносчики, один или несколько параметров которых изменяется по закону первичного (основного) сигнала. Применяются два типа переносчиков: – во-первых, гармонические колебания; – во-вторых, периодические последовательности импульсов. Процесс изменения параметров переносчика под воздействием первичного сигнала называется модуляцией. Для гармонических колебаний основные виды модуляций: АМ – амплитудная; ЧМ – частотная; ФМ – фазовая. Есть и другие виды: балансовая – БМ, однополосная – ОМ. Они отличаются способами преобразования амплитуды и сдвигом фазы. На практике применяются также системы с двойной модуляцией ОМ-АМ, ФМ-АМ, ЧМ-АМ, ЧМ-ОМ, ЧМ-ЧМ и др. Несущая может модулироваться дискретным сообщением. В этом случае говорят о дискретных АМ, ЧМ, ФМ. Используется также ОФМ – относительная фазовая модуляция, при которой фаза отсчитывается не от эталона, а от фазы предыдущего сигнала. При использовании периодической последовательности импульсов модуляция называется импульсной – ИМ. Основные виды ИМ: 1. АИМ – амплитудно-импульсная модуляция (рис. 2.5). АИМ не нашла широкого применения из-за низкой помехоустойчивости
t Рис.2.5. Амплитудно-импульсная модуляция 2. ШИМ – широтно-импульсная модуляция (рис. 2.6).
U
t Рис.2.6. Широтно-импульсная модуляция изменяется ширина, т.е. длительность импульсов. Модуляция помехоустойчивая и имеет широкое применение. 3. ФИМ – фазоимпульсная или времяимпульсная модуляция (ВИМ) (рис. 2.7).
t 0 1 2 3 4 5 6 7 Рис.2.7. Фазоимпульсная или времяимпульсная модуляция отсчет относительно тактовых точек, амплитуда – постоянная. 4. ЧИМ – частотно-импульсная модуляция. Изменяется частота импульсов по закону следования изменения первичного сообщения. 5. КИМ – кодоимпульсная модуляция. Передаваемое сообщение квантуется по времени и амплитуде, каждому уровню присваивается своя кодовая комбинация. До КИМ была ЧИМ – число импульсная модуляция, при изменении величины U(t) менялось число передаваемых импульсов. Это основные виды, но есть и другие виды, например: дельта-модуляция – если функция U(t) увеличивается, то импульсы есть, если уменьшается, то импульсов нет. Есть многократная модуляция ШИМ-АИМ, ФИМ-АИМ – дополнительно меняется также и амплитуда сигнала. Кодирование
Передаче подлежит не только количественная информация, но и команды типа: “вкл.-выкл.”, “авария”, “открыто-закрыто” и т.п. Основным способом передачи такой информации является кодирование, т.е. применение кодоимпульсных или цифровых систем. Кодирование – это универсальный способ отображения любого вида информации при ее передаче, обработке и хранении. Основные достоинства: высокая точность отображения; высокая помехоустойчивость; возможность обработки на ЭВМ. Самое простое определение кодирования: кодирование – это сопоставление дискретному сообщению ai (i=1...k) определенной последовательности n кодовых символов bj(j=1...m), где n – число разрядов кода; m – число используемых признаков сигнала или основание кода. Если число разрядов n во всех кодовых комбинациях одинаковое (n = const), то код называется равномерным и общее число комбинаций, а следовательно, сообщений равно N = mn. (2.1) Если n ≠ const, то код называется неравномерным и общее число кодовых комбинаций зависит от способа кодирования. Совокупность символов bj называется кодовым алфавитом. Совокупность кодовых комбинаций называется языком. Совокупность правил составления кодовых комбинаций называется синтаксисом кода. Выбор способов кодирования (m, n, а также синтаксис) зависит от специфики АСУ ТП. Основные критерии выбора: – экономичность отображения информации; – простота технологической реализации; – удобство обработки и хранения; – надежность передачи и др. – обнаружение и исправление ошибок, распознавание объектов. Очевидно, наиболее удобным и пригодным будет цифровой код с определенным числом "m" и "n" и определенным синтаксисом. Например: для передачи 1000 сообщений в коде с основанием 10 потребуется 3 разряда 103 = 1000 (0,1,2...999), а в коде с основанием 2 – 10 разрядов 210 = 1024. На первый взгляд передача десятью разрядами сложнее, громоздче, чем тремя. Но если подсчитать общее число использованных знаков в первом и втором случае, то получим 10∙3 = 30 и 2∙10 = 20. Следовательно, более удобным оказался 2-й код. А самым удобным будет очевидно тот код, у которого для передачи одного и того же количества сообщений будет минимально произведение m∙n: m∙n → min. Найдем это число из равенства (2.1). Число разрядов n зависит от N, то есть необходимо искать min по m. Для этого сначала прологарифмируем выражение (2.1): n=ln N / ln m → ln N=n∙ln m. Умножим обе части на m: m∙n=m∙ln N / ln m. Для нахождения m∙n = min берем производную по m от правой части и приравниваем ее к нулю. Вывод выполняем по схеме
тогда ln m – 1 = 0, ln m = 1, m = e ≈ 2,72. Хотя m=3 ближе к оптимальному значению, но из соображений простоты технической реализации устройств передачи, хранения и особенно обработки информации используется m = 2. В нашей стране разрабатывалась вычислительная техника с m = 3, но она не выдержала конкуренции с уже налаженной двоичной системой. Необходимое число разрядов для записи двоичным кодом некоторого числа A: n ≈ log2 A. Принимается ближайшее большее значение. Если m не 2, то n = logm A – также ближайшее большее. При вводе – выводе информации в АСУ ТП или ЭВМ для компактности записи используют коды, основания которых кратны целой степени числа 2: 23 = 8 – восьмеричный код; 24 = 16 – шеснадцатеричный код, которые в АСУ ТП или ЭВМ все равно переводятся в двоичный код. Наиболее удобен цифровой алфавит, для которого любое число можно представить выражением
где m – основание системы счисления; n – количество разрядов; i – номер разряда; ki – разрядный коэффициент, ki = 0, 1, 2, … m – 1. Наиболее распространена десятичная система, например: А10 = 59310= 5∙102 + 9∙101 + 3∙100. Если индекс 8, то система восьмеричная: А8= 23578= 2∙83 +3∙82 +5∙81 +7∙80 и т. д. Для работы необходимо знать правила перевода чисел из одной системы в другую.
Поиск по сайту: |

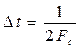 ,
,
 .
. ,
,  .
.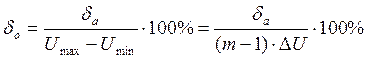 .
.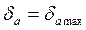 ,
,  .
. U
U
 U
U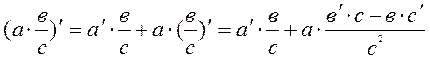 ,
, , (2.2)
, (2.2)