 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные положения алгебры логики
Любая переменная, любая функция принимает два значения: 0 и 1. Отношения между этими значениями определяются тремя логическими операциями и отношением эквивалентности: 1. Логическое сложение (дизъюнкция), обозначается с помощью знаков "+" или "Ú", реализуется логическим элементом ИЛИ. 2. Логическое умножение (конъюнкция), обозначается с помощью знаков "×" или "Ù", реализуется логическим элементом И. 3. Логическое отрицание (инверсия), обозначается с помощью знаков " - " или 4. Эквивалентность, обозначается с помощью знака "=". При выполнении всех операций отношение эквивалентности определяется следующими выражениями:
Законы двоичной алгебры. I. Законы одинарных элементов: а) универсального или единичного множества
б) нулевого множества
II. Законы отрицания: а) основной б) дополнительности в) двойственности III. Комбинационные законы: а) тавтологии б) коммутативные или переместительные законы
в) ассоциативные или согласовательные законы
г) дистрибутивные или распределительные законы
д) адсорбции или поглощения
е) склеивания
Из этих законов вытекает, что двоичная алгебра дуальна относительно сложения и умножения. Это свойство закона двойственности было установлено Морганом и обобщено Шенноном в теореме: “инверсия произвольной комбинации двоичных переменных, связанных законами дизъюнкции и конъюнкции, эквивалентна замене в ней значений переменных их инверсиями при одновременной смене знаков "+" на "×" и "×" на "+"”. Например:
Функции двоичной алгебры обозначаются, как и в обычной алгебре
но называются иначе – переключательные функции (ПФ) и записываются в виде двоичных аргументов, соединенных знаками логических операций. Аргументы переключательной функции
Это положение называется принципом суперпозиции. Полный набор элементов, с помощью которых можно реализовать любую функцию, состоит из трех логических элементов " И ", " ИЛИ ", " НЕ " (функционально полный набор). Установлено, что переключательные функции можно реализовать и с помощью одного элемента с минимальным функционально полным набором "И-НЕ" (элемент Шеффера – реализует функцию С помощью законов двоичной алгебры можно осуществлять однозначный переход из одного базиса в любой другой.
Поиск по сайту: |
, 
, 
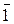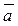, реализуется логическим элементом НЕ.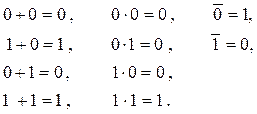
,
сами могут быть переключательными функциями других аргументов:
) или с помощью одного элемента "ИЛИ-НЕ" (элемент Пирса – реализует функцию 
). Эти наборы составляют основу микроэлектроники.