 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аналитические методы получения математических моделей непрерывных одномерных и многомерных объектов автоматизации
Аналитические методы базируются на знании фундаментальных закономерностей электромеханического преобразования энергии (физика, математика, ТОЭ, электроника, электрические измерения, электрические машины, электрический привод, ТСА, ТАУ и др.). Согласно ТАУ, любая сложная структура может быть разбита на отдельные элементы, уравнения которых известны или легко выводятся. Например: электрическая цепь при последовательном соединении R:
где q – заряд; i – ток. Изучали и механические цепи, и усилители, и преобразователи, и двигатели, выводили их зависимости. Запишем, например, зависимость скорости двигателя постоянного тока независимого возбуждения от напряжения якоря Во-первых, запишем уравнение для напряжения, приложенного к якорю:
Во-вторых, вспомним, чему равна Э.д.с. якоря
Связь тока якоря со скоростью найдем через связь момента двигателя с током якоря и скоростью вращения якоря. Известно, что:
отсюда
После подстановки выражений для э.д.с. и тока в уравнение для Uя имеем:
Уравнение второго порядка можно упростить, перевести в операторную форму, можно найти зависимость ω = f(Uв), но нужны другие формулы. Если объект (система) имеет один вход и один выход и известна его структура, то с помощью известных правил преобразования структурных схем можно получить математическую модель объекта в виде дифференциального уравнения, порядок которого определяется числом накопителей энергии в объекте. Такие правила изучались в курсе ТАУ. Реальные объекты, как правило, являются многомерными (многосвязными), имеющими несколько входов и несколько выходов. В подобных системах изменение одного управляющего или возмущающего воздействия вызывает изменение нескольких управляемых переменных, а каждая управляемая переменная зависит от нескольких управляющих и возмущающих воздействий. В многоканальных системах входные воздействия, возмущающие воздействия и выходные переменные описываются как многомерные векторы, связанные некоторым оператором преобразования. Из математики известно векторное выражение переменной:
Если возможен перенос возмущений к выходу объекта, то уравнение (3.1) можно переписать в виде
а при идентификации объекта – только по управляющим воздействиям (
Здесь оператор преобразования Ф аналогичен передаточной функции W в одноканальных системах. В многоканальных системах решаются те же задачи, что и в одноканальных, т.е. стабилизация, программное и следящее управление, оптимизация. Для них также важно определение устойчивости, качества динамических процессов. Структура многоканальных систем тоже может быть представлена в виде отдельных элементов с прямыми и обратными связями. С помощью известных правил можно преобразовать, упрощать схему, вводить корректирующие элементы. Уравнение (3.2) в развернутом виде записывается как система. Например, при трех управляющих воздействиях х1 - х3 и трех выходных переменных у1 - у3:
Здесь аi – статические коэффициенты передачи, вещественные коэффициенты для статической характеристики или передаточные функции, операторные полиномы для уравнений динамики. Пример такой системы приведен на рис.3.1.
Х2(р) Y2(р)
Х3(р) Y3(р)
Рис. 3.1. Структура многоканальной системы
Описание системы без связи Н8 имеет вид
Решить систему обычным способом, особенно для динамики, очень сложно. С увеличением числа входов и выходов задача более усложняется. Поэтому для получения компактных форм представления моделей многомерных систем применяется матричная форма записи переменных и операторов преобразования, т.е. системы (3.3) или (3.4) записываются в виде Y=A·X. Под матрицей понимается упорядоченная, т.е. выполненная по определенному правилу, табличная форма записи цифр, буквенных коэффициентов или передаточных функций и полиномов. Матрицы Y, X, A:
где Y и X – соответственно матрицы входных и выходных переменных; A – матрица передаточных функций или передаточная матрица. При наличии некоторых навыков операции с матрицами воспринимаются легче, чем операции с множеством переменных. Математическое обеспечение современных ЭВМ также располагает программами, ориентированными на унифицированное матричное представление задач анализа и синтеза многомерных систем. Специфические особенности многомерных систем – это неравенство числа входов и выходов, обычно ny > nx , а также взаимовлияние каналов друг на друга. Например, в приведенной схеме x1 влияет на y1и на y3 через связь в виде элемента Н6. Ели это влияние является объективным проявлением естественных свойств объекта, то такая связь называется естественной. Если связь введена специально, например, для нейтрализации взаимного влияния, то она называется искусственной или корректирующей. Так, для исключения влияния x1 на y3 необходимо на вход x3 подать с входа x1 корректирующую связь с передаточной функцией
взятую со знаком минус. Тогда
или
Теперь y3 не зависит от x1. Чтобы исключить влияние x2 на y3, нужно подать на x3 корректирующую связь Н9 (на схеме не показана) также со знаком минус:
Система (3.4) в виде матрицы имеет вид
где Н(р) – передаточная матрица аналогичная матрице
Если скорректировать влияние x1, x2 на y3, то элементы а31 и а32 станут равными 0. Диагональные элементы передаточной матрицы называются собственными передаточными функциями, т.к. отражают зависимость каждого выхода от своего входа. Обозначаются они, для отличия от других элементов, буквой М. Остальные элементы передаточной функции называются несобственными и обозначаются буквой L. То есть
Очевидно, чтобы каналы стали автономными (тогда легче выполняются расчеты и легче управление) матрица должна стать диагональной. Из матрицы легко определяют корректирующие связи. Таким образом, при идентификации объектов можно не только получать их описание, но и каким-то образом влиять на это описание:
Для исследования многомерных объектов, как и для одномерных, применяются классические частотные и временные методы. При частотных методах, если на один из входов подается гармонический сигнал частоты ω, то на всех выходах появляется гармонический сигнал той же частоты, но с другими амплитудами и фазами, т.е. вводятся понятия собственной и несобственной амплитудно-фазовой характеристики. При временных методах исследования рассматривают не уравнения (3.3), а переходную матрицу, отображающую временную реакцию выходов объекта на единичные скачки на выходах. Векторно-матричная форма описания многомерных объектов применяется и при описании их в пространстве переменных состояний (метод пространства состояний). При этом упрощается расчет и анализ на ЭВМ. Надо отметить, что на результаты идентификации решающее влияние оказывает выбор исходной модели, определение числа входов и выходов, потому что до выполнения анализа неизвестна значимость отдельных входов. В этом плане различают полностью управляемые объекты, когда все входы зависят от всех выходов, и полностью наблюдаемые объекты, когда нет переменных состояний, не связанных с выходами.
Поиск по сайту: |
 , или
, или  ,
, . Эти зависимости можно вывести.
. Эти зависимости можно вывести. .
. .
. и
и  ,
, .
.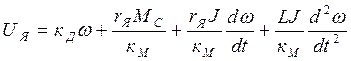 .
. . (3.1)
. (3.1) ,
, = 0), замкнутое управление – по отклонению:
= 0), замкнутое управление – по отклонению: . (3.2)
. (3.2)
 ,
, , (3.3)
, (3.3) .
. Х1(р) Y1(р)
Х1(р) Y1(р)

 ,
, ,
, (3.4)
(3.4) .
. ;
;  ;
;  ,
, ,
,
 .
. .
.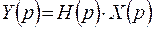 ,
, ,
, .
. . (3.5)
. (3.5)
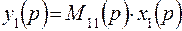 ,
, ,
, .
.