 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритмы управления состоянием объекта
В общем случае задача синтеза системы управления сводится к тому, чтобы для заданного многомерного объекта по полученной модели и определенным требованиям к качеству управления, при известной системе возмущений и ограничений, определить структуру и параметры такого многомерного регулятора, который обеспечит необходимое качество управления. Такая задача решается как вариационная, путем последовательных приближений, когда качество управления представляется в виде функционала от управляющих и возмущающих воздействий. Достижение экстремальных значений этого функционала является решением задачи многомерной оптимизации. Рассмотрим сущность принципа инвариантности. Она заключается в компенсации возмущений введением дополнительных каналов действия, по которым проходят инвариантные компенсирующие действия возмущений в виде сигналов, пропорциональных этим возмущениям. В автоматике этот принцип известен как принцип Б. Н. Петрова. Наиболее просто он реализуется по отношению к задающему воздействию. Например, имеется трехмерная система
или в виде матричного уравнения
Если пренебречь возмущениями, то можно записать
Отсюда
или в развернутом виде
Чтобы система (4.3) стала автономной (инвариантной), матрица коэффициентов должна быть диагональной, то есть
тогда
Эта задача решается введением дополнительных компенсирующих каналов. Для примера, компенсируем влияния 1 и 2 каналов на выходную величину 3-го канала. Компенсирующие коэффициенты обозначим
Для инвариантности системы необходимо, чтобы
Аналогичные рассуждения применимы и к независимым внешним воздействиям типа возмущений. Усложняет задачу только необходимость измерений возмущений. Но бывают возмущения, которые невозможно измерить (внутренние переменные, случайные воздействия), тогда инвариантность осуществляется путем учета изменений выходных переменных, т. е. введением обратных связей. Возьмем ту же систему (4.1), но в несколько упрощенном виде
Рассмотрим второе инвариантное уравнение. Для того чтобы
Для инвариантности уравнения необходимо, чтобы
Тогда
Действие возмущений уменьшилось в (
Поиск по сайту: |
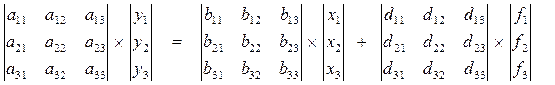 (4.1)
(4.1)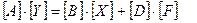 . (4.2)
. (4.2)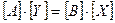 .
.
 . (4.3)
. (4.3)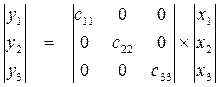 ,
,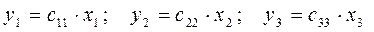 .
. и
и 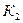 соответственно. Тогда матрица (4.3) принимает вид
соответственно. Тогда матрица (4.3) принимает вид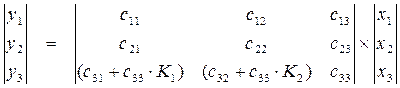 .
.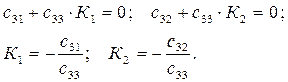
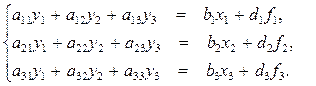 (4.4)
(4.4)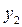 зависел от
зависел от 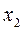 и мало зависел от
и мало зависел от 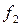 , необходимо подать сигналы перекрестных связей на
, необходимо подать сигналы перекрестных связей на  с
с 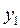 и
и  , а также применить отрицательную обратную связь по
, а также применить отрицательную обратную связь по 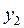 . Тогда второе уравнение системы (4.4) примет вид
. Тогда второе уравнение системы (4.4) примет вид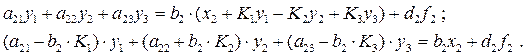
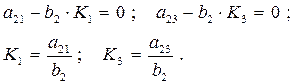

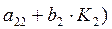 раз.
раз.