 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Идентификация многомерных объектов по экспериментальным данным
Многомерный объект отличается от одномерного тем, что у него много входных и много выходных переменных и существуют перекрестные связи между большинством этих переменных. Для них затруднена или невозможна геометрическая интерпретация модели, т.к. при двух влияющих факторах на выходную переменную приходится обращаться к двухмерной области. При большем числе влияющих факторов рассматриваются многомерные гиперповерхности, не имеющие геометрического смысла. В этом случае целью эксперимента является поиск экстремальных точек (max, min) на этой поверхности, т.е. поиск параметров оптимального управления (при каких хi получаются наилучшие значения уj). Такая модель называется целевой функцией или поверхностью отклика. Получить ее по результатам эксперимента также очень сложно, обычно ограничиваются некоторым приближением. Экстремумы ищут в ограниченной области допустимых значений хi и уj при игнорировании несущественных факторов и при линейном или максимум квадратичном приближении, т.е. замена реальной поверхности отклика линейным или квадратичным полиномом от влияющих факторов. Метод, позволяющий получить многомерную модель объекта управления на основе эксперимента, получил название факторного анализа, в литературе называется еще факторным экспериментом или методом планирования эксперимента. Применительно к детерминированному объекту метод заключается в следующем: 1. Определяются факторы хi, влияющие на выходные параметры уj, определяются области изменения хi и уj. 2. Выбирается тип модели. 3. Планируется объем или составляется программа эксперимента. 4. Выполняется эксперимент, т.е. принудительно изменяются хi в избранных пределах и сочетаниях и измеряются соответствующие уj. Эксперимент всегда активный. 5. Рассчитываются коэффициенты уравнений модели. 6. Выполняется проверка значимости коэффициентов. 7. Выполняется проверка адекватности модели объекту. Некоторые рекомендации для успешного проведения эксперимента: во-первых, необходимо, чтобы входные переменные были независимы друг от друга; во-вторых, необходимо, чтобы точность задания хi была выше точности измерения уj. По аналогии с одномерными объектами определяются центры варьирования переменных х10, х20 … Входные переменные обязательно измеряются в относительных единицах при симметричных значениях хi относительно х0, чтобы убрать нечетные степени. При таком подходе ось у помещается в центр идентифицируемой области, для которой
В качестве базовой величины для всех входных переменных обычно принимается предельное ее отклонение
Тогда в относительных единицах
Модель наибольшей сложности имеет вид
где уj – одна из выходных переменных. Входных переменных две. Это при двух влияющих факторах. Если их будет три, то появятся члены уравнения с Для унификации записи модели все члены уравнения, содержащие переменные хi, х2i и произведения переменных записываются в линейном виде
где х0 – фиктивная переменная, очевидно х0 = 1;
Таких уравнений будет столько, сколько выходных переменных у. В общем, виде это уравнение можно записать:
где п – число членов уравнения регрессии. После выбора типа модели определяется объем эксперимента: устанавливается, сколько раз, в какой последовательности и в каких различных сочетаниях надо изменять хi, чтобы получить достаточно достоверный результат при минимальном объеме эксперимента. Для определения коэффициентов ai, в соответствии с принципом минимума суммы квадратов отклонении, сначала для выходных переменных записываются функционалы
где N – число опытов. Коэффициенты ai определяются также из системы уравнений для частных производных по полученным в результате эксперимента значениям уэ и хэ:
Есть также способы упрощенного определения коэффициентов с применением определенных допущений и матричной записью исходных данных.
Поиск по сайту: |
 .
. или
или 
 ,
, ,
, .
. ,
, ,
,  ,
, 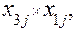

 .
.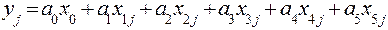 ,
, ,
,  ,
,  .
. , (3.10)
, (3.10)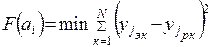 ,
, .
.