 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статическая оптимизация линейных и нелинейных детерминированных объектов
Предполагается, что объект достаточно хорошо изучен, получены аналитическая модель объекта и выражения для целевых функций. Все функции непрерывны, детерминированы и имеют производные в любой точке. Для управления принята разомкнутая система, т.к. для замкнутой все выкладки значительно усложняются. Методика получения параметров оптимального управления следующая. Записывается уравнение или система уравнений модели управляемого объекта. Это могут быть уравнения линейной регрессии вида
Записываются уравнения целевых функций Fk с учетом выбранных критериев эффективности работы объекта. Например, при оптимизации по качеству продукции целевая функция представляется как сумма квадратов отклонений управляемых технологических параметров от заданных значений:
где yjз – заданное значение управляемого параметра (зольность, кусковатость и т.п.). А нам нужны зависимости от xi. Поэтому из выражений целевых функций исключаются текущие значения yj подстановкой в них уравнений модели. С учетом весовых коэффициентов выражение для обобщающей или общей целевой функции имеет вид
Приравнивая к нулю частные производные вида
где yjз – необходимые значения выходных параметров. Тот ли это экстремум, определяют по знаку второй производной в данной точке d2G / dxi2. При положительном значении – max, при отрицательном – min. При оптимизации сложных и особенно нелинейных многомерных объектов получение надежных уравнений модели, а также уравнений целевых функций и технически сложно, и экономически не всегда целесообразно. Там наибольшее применение нашли градиентные методы нахождения частичных оптимумов по некоторой программе. Управляющее устройство в результате пошагового изменения управляющих переменных обеспечивает поиск и достижение экстремума целевой функции. В процессе управления все время меняется направление и величина шага. Система большее время находится в поиске, пока не приходит в экстремальную точку. Такое управление без применения средств вычислительной техники невозможно. ЗАКЛЮЧЕНИЕ
Построение систем управления связано с определенными трудностями. Все известные, строго установленные результаты касаются лишь узкого класса объектов (в основном статических или линейных динамических) при специально выбранных показателях качества. В то же время инженерная практика «поставляет» проблемы, не соответствующие строгим формулировкам. В отличие от математика, инженер не имеет права отказаться от решения задачи управления на том основании, что для нее отсутствуют теоретические «заготовки» или она не поддается строго обоснованному решению. Инженер должен четко сознавать, что любое математическое описание объекта в определенной мере условно. Его сила зависит от той ситуации, в которой будет работать объект, а она заведомо не в полной мере известна. Как правило, приходится полагаться лишь на интуицию, вбирающую в себя опыт работы со сходными по своей природе объектами. Необходимая полнота математического описания объекта зависит от используемого закона управления. Чем быстрее изменяется управление, тем более подробным должно быть динамическое описание, тем выше должен быть порядок уравнений, описывающих объект. Чем более широк диапазон уровней управляющих воздействий, тем детальнее должно быть математическое описание. Также не следует считать, что закон управления, построенный на базе того или иного «строго доказанного» результата, действительно будет хорошо работать на практике, а с другой стороны, не следует считать, что закон управления, для которого нет «строгого обоснования», не должен практически применяться. Сама теория управления, как техническая наука, не должна исключать из рассмотрения те рекомендации «изобретательского» характера, которые не обоснованы как «оптимальные» по какому-либо четко сформулированному единому критерию. Окончательные оценки инженерной работы по созданию систем управления можно поставить только на основании достаточно длительной эксплуатации системы в реальных условиях. Такая оценка включает множество показателей, каждый из которых по-своему характеризует систему.
Поиск по сайту: |
 .
.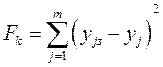 ,
,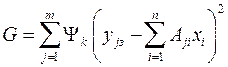 .
. и решая систему уравнений относительно xi , находят параметры оптимального уравнения
и решая систему уравнений относительно xi , находят параметры оптимального уравнения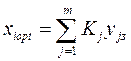 , (4.9)
, (4.9)