 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Параллельный колебательный контур
Параллельный колебательный (резонансный) контур состоит из параллельно соединенных индуктивности L и емкости C, а в цепи индуктивности включено сопротивление ее потерь R. Для параллельного колебательного контура удобнее искать проводимость:
Для резонансной частоты
На резонансной частоте входное сопротивление максимально по модулю, чисто активно и равно R0. На частотах выше резонансного сопротивление имеет емкостной характер, на частотах ниже резонансного – индуктивный характер. Отношение действующего значения тока реактивного элемента к входному току параллельного колебательного контура на резонансной частоте называется добротностью параллельного колебательного контура:
Можно дать другое определение добротности: добротность равна умноженному на 2π отношению энергии, запасенной в контуре, к энергии, рассеиваемой за один период. Данное определение добротности справедливо не только для контуров с сосредоточенными индуктивностями и емкостями, но и для контуров с распределенными индуктивностями и емкостями, например коаксиальных контуров и объемных резонаторов. Величина, обратная добротности, называется затуханием контура: Аналитически АЧХ параллельного контура отражается зависимостью нормированного по резонансному сопротивлению модуля входного сопротивления от величины абсолютной расстройки:
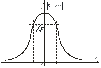
Резонансная характеристика (в параллельном контуре) – нормированное напряжение (его зависимость от частоты) при постоянном токе через контур. ФЧХ параллельного контура определяется следующим выражением:
Частотный коэффициент передачи контура по току нетрудно определить, вычислив отношение тока емкости (индуктивности) к входному току. На резонансной частоте этот параметр выразится формулой:
Итак, на резонансной частоте ток в параллельном контуре в Q раз больше входного тока. Поэтому говорят о резонансе токов в параллельном контуре. Полоса пропускания параллельного контура определяется формулой:
достигает экстремума, то в окрестности этой точки сопряженный сигнал проходит через нуль. Отметим, что преобразования Гильберта имеют нелокальный характер: поведение сопряженного сигнала в окрестности какой-либо точки зависит от свойств исходного сигнала на всей оси времени, хотя наибольший вклад дает, конечно, достаточно близкая окрестность рассматриваемой точки. В последнее время методы, основанные на понятиях аналитического сигнала и преобразований Гильберта, прочно вошли в арсенал теоретической радиотехники.
Поиск по сайту: |
 Выделение полезного сигнала из смеси различных побочных сигналов и шумов осуществляется частотно-избирательными линейными цепями, которые строятся на основе колебательных контуров. Простейшим полосовым фильтром является колебательный контур, образованный элементами R, L и C. В теории цепей подробно изучаются последовательные и параллельные контуры.
Выделение полезного сигнала из смеси различных побочных сигналов и шумов осуществляется частотно-избирательными линейными цепями, которые строятся на основе колебательных контуров. Простейшим полосовым фильтром является колебательный контур, образованный элементами R, L и C. В теории цепей подробно изучаются последовательные и параллельные контуры.
 .
.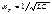 и большой добротности контура Q>>1 справедливо неравенство
и большой добротности контура Q>>1 справедливо неравенство  . В этом случае:
. В этом случае: .Здесь ξ – обобщенная расстройка, определяемая по выражению
.Здесь ξ – обобщенная расстройка, определяемая по выражению  , а
, а – резонансное сопротивление параллельного контура (полное сопротивление контура при резонансной частоте между точками параллельного включения индуктивности и емкости).
– резонансное сопротивление параллельного контура (полное сопротивление контура при резонансной частоте между точками параллельного включения индуктивности и емкости).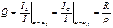 ,Формула Томсона:
,Формула Томсона: 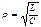 .
. .
.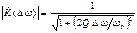


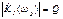
 .
.