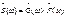|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства преобразований Фурье
1. Свойство линейности. Если имеется некоторая совокупность сигналов s1(t), s2(t),…, причем s1(t)↔S1(ω), s2(t)↔S2(ω),…, то взвешенная сумма сигналов преобразуется по Фурье следующим образом: 2. Теорема запаздывания: Предположим, что для сигнала s(t) известно соответствие s(t)↔S(ω). Рассмотрим такой же сигнал, но возникший на t0 позднее
Модуль комплексного числа 3. Изменение масштаба по оси времени: Рассмотрим сигнал
4. Дифференцирование сигнала: Пусть Таким образом, дифференцирование сигнала эквивалентно умножению его спектра на 5. Интегрирование сигнала: Пусть Следовательно, интегрирование сигнала эквивалентно делению его спектра на величину 6. Теорема о свертке: Рассмотрим сигнал, являющийся сверткой двух сигналов (
Следовательно, спектр свертки двух сигналов равен произведению их спектров. 7. Спектр произведения сигналов: Вследствие взаимной обратимости частоты и времени спектр сигнала, равный произведению двух сигналов должен представлять собой свертку их спектров:
8. Теорема Релея: Скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей.
9. Равенство Парсеваля: Равенство Парсеваля утверждает, что энергия, заключенная в сигнале s(t), равна сумме энергий всех составляющих его спектра.
Равенство Парсеваля характеризует важное свойство сигналов. Если некоторая избирательная система пропускает только часть спектра сигнала, ослабляя другие его составляющие, то это означает, что часть энергии сигнала теряется. Энергия сигнала есть результат интегрирования энергетического спектра сигнала по всему диапазону частот от -∞ до ∞. Иначе говоря, энергия равна площади, заключенной между кривой, изображающей энергетический спектр сигнала, и осью абсцисс.
Поиск по сайту: |
 , ai – произвольные числовые коэффициенты.
, ai – произвольные числовые коэффициенты. :
:
 при любых t0 равен единице, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена в частотной зависимости аргумента его спектральной плотности (фазовом спектре).
при любых t0 равен единице, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена в частотной зависимости аргумента его спектральной плотности (фазовом спектре). , умножение времени t на постоянный коэффициент a эквивалентно изменению масштаба времени.
, умножение времени t на постоянный коэффициент a эквивалентно изменению масштаба времени. Таким образом, уменьшение длительности импульса любой формы в a раз сопровождается расширением его спектра во столько же раз, и наоборот.
Таким образом, уменьшение длительности импульса любой формы в a раз сопровождается расширением его спектра во столько же раз, и наоборот.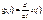 , тогда:
, тогда:  ,
,  - оператор дифференцирования.
- оператор дифференцирования.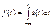 , тогда:
, тогда: 
 ):
):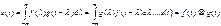
 Найдем спектр такого сигнала:
Найдем спектр такого сигнала: ,
,