 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модулированные сигналы. Сигналы с угловая модуляцией
Модуляцией колебаний называется медленное по сравнению с периодом колебаний изменение амплитуды, фазы или частоты колебаний по определенному закону. Такое изменение осуществляется для того, чтобы с помощью радиочастотного колебания передавать сообщения: речь, музыку, изображение и т.д. Радиочастотные колебания характеризуются амплитудой, частотой и фазой. Соответственно различают три основных вида модуляции: амплитудную, частотную и фазовую. Угловая модуляция.
Аргумент гармонического колебания (полная фаза): Где ω0 – значение частоты в отсутствие полезного сигнала, k – некоторыйкоэффициент пропорциональности. Модуляцию, отвечающую данному соотношению называют фазовой модуляцией (ФМ):
Естественными параметрами ЧМ- сигнала общего вида является девиация частоты ∆ω. Если s(t) – достаточно гладкая функция, то внешне осциллограммы ФМ- и ЧМ- сигналов не отличаются. Однако имеется принципиальная разница: фазовый сдвиг между ФМ- сигналом и немодулирующим колебанием пропорционален s(t), в то время как для ЧМ- сигнала этот сдвиг пропорционален интегралу от передаваемого сообщения. В случае однотонального ЧМ- сигнала мгновенная частота:
Полная фаза такого сигнала: где φ0 – некоторый постоянный фазовый угол. Отсюда видно, что величина Аналитическая форма записи однотонального ФМ- сигнала будет аналогичной. Однако: ЧМ- и ФМ- сигналы ведут себя по разному при изменении частоты модуляции и амплитуды модулирующего сигнала. При частотной модуляции девиация частоты ∆ω пропорциональна амплитуде низкочастотного сигнала. В то же время величина ∆ω не зависит от частоты модулирующего сигнала. В случае фазовой модуляции ее индекс β оказывается пропорциональным амплитуде низкочастотного сигнала независимо от его частоты. Как следствие этого, девиация частоты при фазовой модуляции линейно увеличивается с ростом частоты. Для простейшего случая однотонального ЧМ- или ФМ- сигнала можно найти общее выражение спектра, справедливое при любом значении индекса модуляции β:
Перепишем формулу так: Отсюда получаем следующую математическую модель ЧМ- или ФМ- сигнала с любым значением индекса модуляции:
Спектр однотонального сигнала с угловой модуляцией в общем случае содержит бесконечное число составляющих, частоты которых равны Начальные фазы боковых колебаний с частотами Рассмотрим случай β<<1.
Таким образом, при β<<1 в спектре сигнала с угловой модуляцией содержится несущее колебание и две боковые составляющие (верхняя и нижняя) на частотах Чем больше индекс функции Бесселя, тем протяженнее область аргументов, при которых эта функция очень мала. Важно отметить, что с ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами k > β+1. Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией: Как правило, реальные ЧМ- и ФМ-сигналы характеризуются условием β>>1. В этом случае: Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно равную удвоенной девиации частоты. Для передачи амплитудно-модулированного сигнала требуется полоса частот, равная 2Ω, т. е. в β раз меньшая. Большая широкополосность ЧМ- и ФМ- сигналов обуславливает их применимость для целей радиосвязи лишь на очень высоких частотах. Однако именно широкополосность приводит к гораздо большей помехоустойчивости сигналов с угловой модуляцией по сравнению с АМ- сигналами.
Поиск по сайту: |
 Рассмотрим модулированные радиосигналы, которые получаются за счет того, что в несущем гармоническом колебании
Рассмотрим модулированные радиосигналы, которые получаются за счет того, что в несущем гармоническом колебании передаваемое сообщение s(t) изменяет либо частоту ω, либо начальную фазу φ; амплитуда Um остается неизменной. Такие сигналы получили название сигналов с угловой модуляцией.
передаваемое сообщение s(t) изменяет либо частоту ω, либо начальную фазу φ; амплитуда Um остается неизменной. Такие сигналы получили название сигналов с угловой модуляцией. Полная фаза ψ(t) связана с сигналом s(t) зависимостью:
Полная фаза ψ(t) связана с сигналом s(t) зависимостью: 
 . Если сигнал s(t)=0, ФМ- колебание является простым гармоническим колебанием. С увеличением значений s(t) полная фаза ψ(t) растет. При уменьшении значений модулирующего сигнала происходит спад скорости роста ψ(t) во времени. В моменты времени, когда сигнал s(t) достигает экстремальных значений, абсолютный фазовый сдвиг между ФМ- сигналом и немодулированным гармоническим колебанием оказывается наибольшим. Предельное значение этого фазового сдвига называют девиацией фазы ∆ψ. Мгновенная частота ω(t) сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени:
. Если сигнал s(t)=0, ФМ- колебание является простым гармоническим колебанием. С увеличением значений s(t) полная фаза ψ(t) растет. При уменьшении значений модулирующего сигнала происходит спад скорости роста ψ(t) во времени. В моменты времени, когда сигнал s(t) достигает экстремальных значений, абсолютный фазовый сдвиг между ФМ- сигналом и немодулированным гармоническим колебанием оказывается наибольшим. Предельное значение этого фазового сдвига называют девиацией фазы ∆ψ. Мгновенная частота ω(t) сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени: При частотной модуляции (ЧМ) сигнала между величинами s(t) и ω(t) имеется связь вида:
При частотной модуляции (ЧМ) сигнала между величинами s(t) и ω(t) имеется связь вида: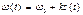 Поэтому
Поэтому 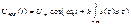 .
.
 ,
, называется индексом однотональной угловой модуляции, представляет собой девиацию фазы такого сигнала, выраженную в радианах.
называется индексом однотональной угловой модуляции, представляет собой девиацию фазы такого сигнала, выраженную в радианах. , Где β – любое вещественное число; Jk(β) – Функция Бесселя k – индекса от аргумента β.
, Где β – любое вещественное число; Jk(β) – Функция Бесселя k – индекса от аргумента β.
 .
. ; амплитуды этих составляющих пропорциональны значениям
; амплитуды этих составляющих пропорциональны значениям  .
. и
и  совпадают, если k – четное число, и отличаются на 180°, если нечетное.
совпадают, если k – четное число, и отличаются на 180°, если нечетное.
 и
и  . Индекс β играет здесь такую же роль, как коэффициент амплитудной модуляции M. Однако можно обнаружить и существенное различие спектров АМ- сигнала и колебания с угловой модуляцией. Для спектральной диаграммы характерно то, что нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180°.
. Индекс β играет здесь такую же роль, как коэффициент амплитудной модуляции M. Однако можно обнаружить и существенное различие спектров АМ- сигнала и колебания с угловой модуляцией. Для спектральной диаграммы характерно то, что нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180°.
 .
.