 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Корреляционный анализ детерминированных сигналов. Спектральная плотность энергии сигнала
Величина Равенство Парсеваля утверждает, что энергия, заключенная в сигнале s(t), равна сумме энергий всех составляющих его спектра.
Для количественного определения степени отличия сигнала s(t) и его смещенной во времени копии s(t-τ) принято вводить корреляционную функцию (автокорреляционную функцию (АКФ))сигнала u(t), равную скалярному произведению сигнала и копии:
Свойства АКФ: 1. При τ=0 автокорреляционная функция становится равной энергии сигнала: 2.Свойство четности: 3. При любом значении временного сдвига τ модуль АКФ не превосходит энергии сигнала: 4. Итак, АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала s(t) автокорреляционная функция может иметь как монотонно убывающей, так и колеблющийся характер. Важную роль играет связь между АКФ и энергетическим спектром сигнала. Квадрат модуля спектральной плотности представляет собой энергетический спектр сигнала. Выражения устанавливающие связь между корреляционной функцией сигнала и его энергетическим спектром, называются соотношениями Винера-Хинчина. Эти результаты принципиально важны по двум причинам. Во-первых, оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток АКФ и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала. Во-вторых, данные формулы указывают путь экспериментального определения энергетического спектра. Часто удобнее вначале получить автокорреляционную функцию, а затем, используя преобразование Фурье, найти энергетический спектр сигнала. Такой прием получил распространение при исследовании свойств сигналов с помощью ЭВМ в реальном масштабе времени. Кроме корреляционной функции можно определить также взаимно корреляционную функцию (ВКФ), которая единым образом описывает как различие в форме сигналов, так и взаимное расположение на оси времени.
Некоторые свойства ВКФ: 1. 2. В отличие от АКФ одиночного сигнала, ВКФ, описывающая свойства системы двух неодинаковых сигналов, не является четной функцией аргумента τ. 3. Если рассматриваемые сигналы имеют конечные энергии, то их ВКФ ограничена. Максимум взаимно корреляционной функции двух одинаковых сигналов имеет место при τ =0. Для различных s1(t) и s2(t) максимум функции может достигать не при τ =0. Взаимно корреляционная функция и взаимный энергетический спектр двух сигналов связаны преобразованиями Фурье.
Поиск по сайту: |
 носит название спектральной плотности энергии сигнала s(t).
носит название спектральной плотности энергии сигнала s(t).
 Энергия сигнала есть результат интегрирования энергетического спектра сигнала по всему диапазону частот от -∞ до ∞. Иначе говоря, энергия равна площади, заключенной между кривой, изображающей энергетический спектр сигнала, и осью абсцисс.
Энергия сигнала есть результат интегрирования энергетического спектра сигнала по всему диапазону частот от -∞ до ∞. Иначе говоря, энергия равна площади, заключенной между кривой, изображающей энергетический спектр сигнала, и осью абсцисс.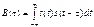 .
.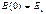 .
. .
.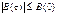 .
. .
. …и…
…и… 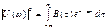 ,
,
 Когда s1(t) и s2(t) – один и тот же сигнал s(t), то взаимно корреляционная и корреляционная функции совпадают.
Когда s1(t) и s2(t) – один и тот же сигнал s(t), то взаимно корреляционная и корреляционная функции совпадают.
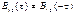

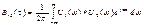 (4.12)
(4.12) - взаимный энергетический спектр сигналов s1(t) и s2(t).
- взаимный энергетический спектр сигналов s1(t) и s2(t).
