 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическое ожидание случайного процесса на входе линейной цепи⇐ ПредыдущаяСтр 12 из 12
Если на входе линейной стационарной системы присутствует колебание X(t), представляющее собой некоторую реализацию случайного процесса X(t); и если эта реализация указана заранее, то к сигналу x(t) следует относиться как к детерминированному. Зная математическую модель системы можно всегда найти выходную реакцию y(t). Однако специфика статистической теории в том, что вместо детерминированного описания входного сигнала мы располагаем лишь сведениями об усредненных вероятностных характеристиках случайного процесса X(t). (плотности вероятности, математическое ожидание, функция корреляции).
X(t) – случайный процесс, стационарный в широком смысле. Найдем математическое ожидание на выходе. Математическое ожидание – среднее значение процесса X(t) в текущий момент времени t, усреднение проводится по всему ансамблю реализаций процесса. Рассмотрим отдельно взятую реализацию X(t), выходной сигнал (согласно интеграла Дюамеля) имеем вид:
Спектральная плотность мощности случайного процесса на выходе линейной цепи. Если на входе линейной стационарной системы присутствует колебание X(t), представляющее собой некоторую реализацию случайного процесса X(t); и если эта реализация указана заранее, то к сигналу x(t) следует относиться как к детерминированному. Зная математическую модель системы можно всегда найти выходную реакцию y(t). Однако специфика статистической теории в том, что вместо детерминированного описания входного сигнала мы располагаем лишь сведениями об усредненных вероятностных характеристиках случайного процесса X(t). (плотности вероятности, математическое ожидание, функция корреляции).
X(t) – случайный процесс, стационарный в широком смысле. Проанализируем линейную цепь в частотной области:
Функция корреляции и спектр мощности стационарного случайного процесса связанны между собой преобразованием Фурье: Корреляционная функция – мера связи между сечениями случайного процесса, взятыми в некоторые моменты времени. Функция W(ω) характеризует удельную меру мощности.
Поиск по сайту: |

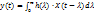 , где h(λ) – импульсная характеристика. Переходя от отдельной реализации к статистическому ансамблю выполняем статистическое усреднение в обеих частях выражения:
, где h(λ) – импульсная характеристика. Переходя от отдельной реализации к статистическому ансамблю выполняем статистическое усреднение в обеих частях выражения: 



 ;
; ;
; .
.