 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие случайного сигнала. Виды случайных сигналов. Характеристики случайных сигналов. Стационарные и эргодические случайные процессы
Случайный сигнал – сигнал носящий случайный характер, т.е. ряд его параметров меняется во времени случайным образом. Случайный процесс может быть представлен неслучайными числовыми характеристиками, постоянными или изменяющимися во времени. Рассмотрим случайный процесс, аналитически описываемый некоторой функцией X(t). Конкретный вид x1(t), x2(t),…,xn(t) этой функции, полученный в результате проведения эксперимента, называют реализацией случайного процесса, совокупность всех реализаций случайного процесса называют ансамблем. Совокупность отдельных мгновенных значений всех реализаций ансамбля в заданный момент времени t1 так же будет некоторой случайной величиной X(t1), называемой сечением случайного процесса. Интегральная функция распределения F(x) – численно определяется как вероятность того, что все значения случайной величины не превышают некоторого заданного уровня x: F(x)=P[X(t1)<x], где P – символ, характеризующий вероятность события. Если величина X(t1) непрерывна во времени, то удобнее пользоваться производной от F(x), которая называется плотностью вероятности: p(x, t1) = dF(x)/dx = dF/x; - это всегда неотрицательная величина и удовлетворяет условию нормировки:
Математическое ожидание Центрированные – случайные процессы с нулевым mx. Дисперсия – характеризует разброс мгновенных значений реализаций случайного процесса относительно его среднего значения. Средне квадратическое отклонение (СКО) – действующее значения случайного напряжения или тока на единичном сопротивлении, а дисперсия – мощность переменной составляющей случайного процесса. Стационарный процесс (в узком смысле) – характеристики случайного процесса не зависят от времени (плотность распределения в любом сечении будет одинакова). Стационарный процесс (в широком смысле) – процесс для которого значение корреляционной функции не зависит от начала отсчета, а зависит только от интервалов времени между сечениями. Эргодический –стационарный процесс, статистические характеристики, которых полученные усреднением по времени стремятся к характеристикам полученным усреднением по ансамблю реализации. Понятие корреляционной функции случайного процесса. Свойства автокорреляционной функции стационарного случайного процесса. Временная автокорреляционная функция эргодического случайного процесса. Функция корреляции представляет собой меру связи между сечениями случайного процесса взятыми в моменты времени t1 и t2.
Когда t1 = t2 функция корреляции численно равна дисперсии: Стационарный процесс – процесс, статистические характеристики которого не меняются во времени. Функция корреляции зависит только от разности τ = t2-t1, поэтому: В случае эргодичного стационарного процесса: эргодический процесс – процесс, при котором усреднение по ансамблю реализации можно заменить усреднением по времени одной реализации в пределах бесконечно длинного интервала Tx. В этом случае:
Если в случайном процессе наблюдается периодичность, то автокорреляционная функция тоже будет периодичной с тем же периодом.
Поиск по сайту: |
 ;
; ; - вероятность попадания в заданный интервал.
; - вероятность попадания в заданный интервал. – среднее значение случайного процесса, полученное в текущий момент времени, усреднением по всему ансамблю реализаций.
– среднее значение случайного процесса, полученное в текущий момент времени, усреднением по всему ансамблю реализаций. ; где σ – СКО.
; где σ – СКО. ;
;
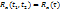 ; из определения стационарности случайного процесса следует, что его функция корреляции является четной относительно τ=0: Rx(τ) = Rx(-τ).
; из определения стационарности случайного процесса следует, что его функция корреляции является четной относительно τ=0: Rx(τ) = Rx(-τ). – временная автокорреляционная функция.
– временная автокорреляционная функция.