 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Последовательный колебательный контур
Последовательный колебательный (резонансный) контур состоит из последовательно соединенных сопротивления r, индуктивности L и емкости С. Как правило, резистор r определяет сопротивление омических потерь провода, из которого выполнена индуктивность. Сопротивление потерь емкости мало и оно на практике не учитывается. Резонансной частотой fр колебательного контура называется частота, при которой реактивная составляющая полного сопротивления колебательного контура: Другими словами, резонансной частоте соответствует равенство реактивных сопротивлений индуктивности и емкости. Из последнего равенства находим выражение для резонансной частоты
Характеристическим сопротивлением ρ называется сопротивление полной индуктивности или емкости контура на резонансной частоте:
Добротностью контура Q называется отношение напряжения на индуктивности UL или на емкости UC к напряжению на активном сопротивлении при резонансе. Поскольку при резонансе напряжение на активном сопротивлении равно ЭДС, действующей в контуре, добротность равна: Можно дать другое определение добротности: добротность равна умноженному на 2π отношению энергии, запасенной в контуре, к энергии, рассеиваемой за один период. Данное определение добротности справедливо не только для контуров с сосредоточенными индуктивностями и емкостями, но и для контуров с распределенными индуктивностями и емкостями, например коаксиальных контуров и объемных резонаторов. Величина, обратная добротности, называется затуханием контура: Преобразуем полное входное сопротивление контура к следующему виду:
где На резонансной частоте входное сопротивление чисто активно и минимально по модулю: Оценим частотно-избирательные свойства колебательного контура. Ток протекающий в контуре, описывается выражением:
Ток Введем понятие частотного коэффициента передачи по току:
Где φ – величина сдвига фазы входного сигнала на выходе контура. При больших добротностях (Q>>1) имеем Найдем модуль частотного коэффициента передачи для малых расстроек частоты: Резонансная характеристика – зависимость амплитуды тока от частоты, нормированная к резонансному току, определенная при постоянном напряжении по контуру. Ширина полосы пропускания АЧХ: Аргумент функции определяется формулой (ФЧХ):
На резонансной частоте:
При настройке контура в резонанс амплитуда напряжения на конденсаторе (или на индуктивности) в Q раз больше амплитуды входного напряжения. Поэтому резонанс в последовательном контуре называется резонансом напряжений.
Поиск по сайту: |
 Выделение полезного сигнала из смеси различных побочных сигналов и шумов осуществляется частотно-избирательными линейными цепями, которые строятся на основе колебательных контуров. Простейшим полосовым фильтром является колебательный контур, образованный элементами R, L и C. В теории цепей подробно изучаются последовательные и параллельные контуры.
Выделение полезного сигнала из смеси различных побочных сигналов и шумов осуществляется частотно-избирательными линейными цепями, которые строятся на основе колебательных контуров. Простейшим полосовым фильтром является колебательный контур, образованный элементами R, L и C. В теории цепей подробно изучаются последовательные и параллельные контуры.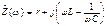 равна нулю:
равна нулю: 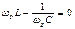 .
. , где
, где  .
. . Подставляя значение резонансной частоты, получаем (формула Томсона):
. Подставляя значение резонансной частоты, получаем (формула Томсона):  .
. .
.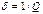 .
. ,
, – обобщенная расстройка.
– обобщенная расстройка. .
.
 в последовательном резонансном контуре, имеющий максимальное значение на частоте резонанса
в последовательном резонансном контуре, имеющий максимальное значение на частоте резонанса  , называют резонансным током.
, называют резонансным током.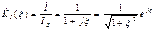 ,
, и обобщенную расстройку можно приближенно записать следующим образом:
и обобщенную расстройку можно приближенно записать следующим образом:  , где
, где  – абсолютная расстройка контура относительно частоты входного сигнала.
– абсолютная расстройка контура относительно частоты входного сигнала.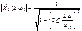

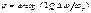


 .
.