 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Спектральный анализ непериодических сигналов. Преобразование Фурье, его основные свойстваСтр 1 из 12Следующая ⇒
Гармонический анализ периодического колебания. Ряд Фурье. Комплексная форма ряда Фурье. Периодический сигнал S(t) – математическая модель процесса, повторяющегося во времени.
Спектральный подход заключается в том, что любое колебание сложной формы заменяется суммой конечного или бесконечного числа гармонических колебаний с соответствующими амплитудами, частотами и фазами. Функция времени заменяется функцией частоты, что во многих случаях является желательным, поскольку хорошо известны частотные характеристики радиоэлектронных устройств. Периодический сигнал можно представить рядом Фурье в виде суммы гармонических составляющих, при этом достаточное условие разложимости сигнала в ряд Фурье (Условия Дирихле): 1. На периоде функция непрерывна или имеет конечное число точек разрыва 1 рода; 2. На периоде функция монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Ряд Фурье для периодического сигнала:
Коэффициенты ряда Фурье:
В общем случае периодический сигнал содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний (гармоник)с частотами Каждую гармонику можно описать ее амплитудой
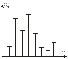
Спектральная диаграмма периодического сигнала (графическое изображение коэффициентов ряда Фурье для конкретного сигнала). Различают амплитудные и фазовые спектральные диаграммы.
Особо интерес представляет амплитудная диаграмма которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала. Ряд Фурье в комплексной форме: Комплексные сигналы будем представлять комплексными числами. Воспользуемся формулами Эйлера:
Подставим полученные выражения в формулу для ряда Фурье:
Далее найдем комплексные коэффициенты ряда Фурье:
Ряд Фурье в комплексной форме:
Связь коэффициентов ряда Фурье в комплексной форме и в обычной форме.
Спектральный анализ непериодических сигналов. Преобразование Фурье, его основные свойства. Если периодическую функцию можно представить рядом Фурье в виде суммы гармонических составляющих, то непериодическую функцию (например если исследуемый сигнал представляет собой одиночный импульс) при выполнении определенных условий можно представить интегралом Фурье. Наглядным является представление об интеграле Фурье как о предельной форме ряда Фурье при стремлении периода функции T к бесконечности. При увеличении периода T расстояние вдоль оси частот между гармониками ряда сокращается и линейчатый спектр в пределе становится непрерывным. Достаточным, но не необходимым условием существования преобразования Фурье является абсолютная интегрируемость функции, т.е.
Формула обратного преобразования Фурье позволяет восстановить сигнал по его спектру:
Если s(t) - действительная функция времени, то |S(w)| - четная функция частоты, а Если Метод спектральных разложений чрезвычайно обогащает теорию сигналов. Например, часто математическая модель сигнала, представленная функцией во временной области, сложна и не достаточно наглядна. В то время описание этого сигнала в частотной области может оказаться простым. Также важно другое: спектральное представление сигналов открывает путь к анализу прохождения сигналов через широкий класс радиотехнических цепей, устройств и систем.
Поиск по сайту: |

 , T – период сигнала.
, T – период сигнала.

 – основная частота последовательности, образующей периодический сигнал.
– основная частота последовательности, образующей периодический сигнал. …..
…..  ….
…. 
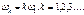
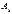 и начальной фазой
и начальной фазой  . Для этого коэффициенты ряда Фурье следует записать в виде:
. Для этого коэффициенты ряда Фурье следует записать в виде: 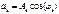 ,
,  , так, что
, так, что  ,
, 
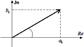 Получим другую, эквивалентную форму ряда Фурье:
Получим другую, эквивалентную форму ряда Фурье: , которая иногда оказывается удобнее.
, которая иногда оказывается удобнее.
 ;
; 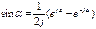
 ;
; 
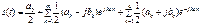
 ;
;  ;
; 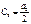
 ; с коэффициентами:
; с коэффициентами: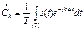
 ,
, 
 Функция
Функция  носит название спектральной плотности сигнала s(t). Данная формула осуществляет прямое преобразование Фурье.
носит название спектральной плотности сигнала s(t). Данная формула осуществляет прямое преобразование Фурье.
 - нечетная функция частоты.
- нечетная функция частоты. – комплексная функция времени, то четность-нечетность не соблюдается.
– комплексная функция времени, то четность-нечетность не соблюдается.