 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Множественность и единство моделей
Реальный объект может иметь несколько разных моделей. Когда архитектор готовится построить новое здание, то прежде чем воздвигнуть его, он сооружает здание из кубиков на столе. Это – модель. Если представлен только чертеж того же проектируемого здания, то это тоже модель. Если есть таблица чисел и формул, на основании которых можно судить о том же здании, то и это – тоже его модель, но в другом исполнении. Реальное здание по отношению ко всем своим моделям является оригиналом или прототипом. Модель – это объект, определенным элементам которого соответствуют элементы другого объекта – оригинала, причем взаимосвязям и отношениям между элементами модели соответствуют определенные взаимосвязи и отношения между элементами оригинала. Указанная выше множественность моделей связана с тем, что каждая их них по-своему отражает отдельные стороны реального объекта, т.е. рассматриваемая система моделей составляет основу суждения об объекте вообще и о здании в частности. И не просто каких-то моделей, а взаимосвязанных. Так, молекулу вещества будет характеризовать система математических моделей, каждая из которых зависит от постановки задачи. Если нужно установить простейшую формулу соединения, то достаточно выразить с помощью взаимно простых чисел индексы при элементах химической формулы. В молекулярной формуле каждый индекс определяет количество атомов соответствующего элемента, структурная формула должна характеризовать строение молекулы, а пространственная модель – еще и её конфигурацию. И эта множественность математических моделей связна с тем, что каждая из них отражает отдельные стороны одного и того же реального объекта, исследует различные системы его свойств. Рассмотрим задачу: Массовая доля углерода в углеводороде составляет 1) Запишем формулу неизвестного углеводорода в виде
значит, 2) Теперь построим математическую модель, определяющую Поскольку в молекуле предельного углеводорода
Итак, для определения натуральных чисел х и у имеем смешанную систему
решая которую, находим: Следовательно, 3) Поскольку углерод в углеводороде четырехвалентен, а водород одновалентен, то
│
│
4) В учебниках химии отмечается, что модель молекулы метана тетраэдрическая, т.е. является правильным тетраэдром, все ребра которого имеют одинаковую длину, а грани являются правильными конгруэнтными треугольниками. Центр такого тетраэдра совпадает с положением атома Пусть точка
и Отметим, что в учебниках химии величина этого валентного угла сообщается догматически.
Рисунок 2.1 – Тетраэдрическая модель молекулы метана
Единство моделей состоит в том, что различные объекты могут иметь одну и ту же математическую модель, например
различные объекты имеют одинаковую математическую модель, то можно один из этих объектов моделировать другим. Так, площадь фигуры, для вычисления которой служит такая математическая модель, как интеграл, можно определить с 2–3 значащими цифрами с помощью взвешивания на аналитических весах. Для этого достаточно вычертить заданную фигуру (её площадь запишем в виде Примечательно, что при моделировании одного объекта другим, их общая математическая модель (в рассмотренном примере – определенный интеграл), посредством которой изучение одного объекта заменяется другим, остается в стороне, хотя именно на единстве математической модели основана возможность такого изучения.
Важнейшим требованием к математической модели является требование ее адекватности…. А.Д. Мышкис
Поиск по сайту: |
 %. Определите: 1) Простейшую формулу углеводорода; 2) Его молекулярную формулу; 3) Структурную формулу;
%. Определите: 1) Простейшую формулу углеводорода; 2) Его молекулярную формулу; 3) Структурную формулу;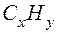 , где
, где 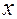 и
и 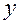 – натуральные числа. По массовой доле углерода в углеводороде составляем уравнение:
– натуральные числа. По массовой доле углерода в углеводороде составляем уравнение:  , т.е.
, т.е.  или
или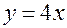 , (2.1)
, (2.1) – простейшая формула углеводорода, так как числа
– простейшая формула углеводорода, так как числа  и
и  – взаимно простые.
– взаимно простые.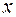 и
и 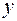 .
.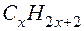 с
с 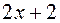 , для индексов
, для индексов 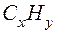 любого углеводорода справедливо неравенство
любого углеводорода справедливо неравенство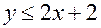 . (2.2)
. (2.2)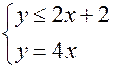 ,
,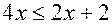 или
или  , но
, но 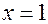 и из уравнения (2.1)
и из уравнения (2.1) .
.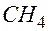 – молекулярная формула углеводорода (метан). Заметим, что в этом случае простейшая формула совпадает с молекулярной.
– молекулярная формула углеводорода (метан). Заметим, что в этом случае простейшая формула совпадает с молекулярной.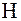
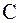 ──
──  и все валентные углы
и все валентные углы 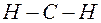 конгруэнтны. Вычислим их.
конгруэнтны. Вычислим их. – центр правильного тетраэдра
– центр правильного тетраэдра  , т.е. центр описанной около него сферы (рисунок 2.1); поэтому
, т.е. центр описанной около него сферы (рисунок 2.1); поэтому  . Обозначим длину ребра тетраэдра как
. Обозначим длину ребра тетраэдра как  , и продолжим
, и продолжим 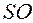 до пересечения с основанием
до пересечения с основанием  . Тогда
. Тогда 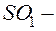 высота, и
высота, и  , так как
, так как  – центр правильного треугольника со стороной
– центр правильного треугольника со стороной 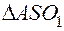 имеем:
имеем: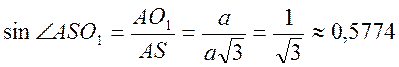
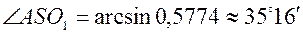 , следовательно,
, следовательно,
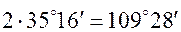 [41, c. 69].
[41, c. 69].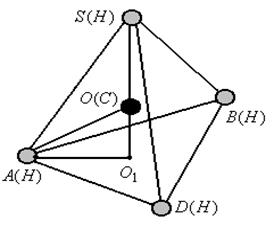
 . Кроме того, если
. Кроме того, если ) на ватмане или тонком картоне, вырезать её и взвесить (вес обозначим как
) на ватмане или тонком картоне, вырезать её и взвесить (вес обозначим как 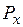 ) затем вырезать из этого же картона единичный квадрат (
) затем вырезать из этого же картона единичный квадрат ( 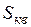 =1), взвесить его (
=1), взвесить его (  – вес единичного квадрата) и написать пропорцию
– вес единичного квадрата) и написать пропорцию