 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
О сущности аксиоматического метода
Прежде чем приступить к решению прикладной задачи мы создаём её математическую модель, перечисляя те особенности, которые будут использованы при решении, т.е. применяем принятый в математике аксиоматический метод: требования, предъявляемые к математической модели, являются аксиомами, лежащими в основании математического решения прикладной задачи. В этой связи хотя бы кратко охарактеризуем сущность аксиоматического метода, с которым все знакомы поскольку, изучая геометрию в школе, нам приходилось исходя из её аксиом и ранее доказанных теорем, выводить другие теоремы логически, дедуктивно, т.е. без обращения к опытному их обоснованию. Однако чтобы разобраться в сущности аксиоматического и связанного с ним дедуктивного метода вовсе нет необходимости строить такие обширные аксиоматические системы как геометрия или алгебра. Ведь уже всякую школьную задачу по математике, физике, химии … можно рассматривать как некую аксиоматическую микросистему, в которой роль аксиом играют исходные данные (а также положения и законы других наук, используемые в процессе решения). Иными словами, всё, что дано по условию – это аксиомы, а любые следствия из них, полученные дедуктивно – теоремы. И даже задача для дошколят «В курятнике было 7 цыплят. Два из него вышли. Сколько цыплят в нём осталось?», если её требуется решить без обращения к натурному эксперименту, т. е. найти результат дедуктивно, логически, уже доставляет нам простой, но выразительный пример аксиоматической микросистемы, состоящей всего из двух аксиом: первая «в курятнике было 7 цыплят» и вторая – «два цыплёнка вышли из курятника». Итак, если в курятнике было 7 цыплят и два из него вышли, то в курятнике осталось 5 цыплят. Вот это утверждение и есть теорема! Заметим, что эту задачу можно решить и экспериментально. Но для этого надо построить экспериментальную установку – курятник: посадить в него 7 цыплят, затем двух выпустить и, наконец, посмотреть, сколько в курятнике осталось цыплят. Думаю, каждый читающий эти строки отдаст предпочтение математическому, дедуктивному методу решения. Оно и экономически эффективнее любого нематематического решения, так как не требует затрат ни времени ни средств. Уже этот пример показывает, что дедуктивный метод не противопоставляется индукции и эксперименту: все методы должны работать во взаимодействии, дополняя друг друга. При решении научных и практических задач часть информации добывается экспериментально, а затем из нее дедуктивно выводятся соответствующие следствия (теоремы). Сила дедуктивного и связанного с ним аксиоматического метода особенно проявляется в том случае, если для получения результата вообще невозможно поставить натурный эксперимент. (Вспомним определение даты боя между лидийцами и мидянами) Дедуктивный метод в той или иной форме используется во всех областях, включая и литературу. Например, широко известный герой, знаменитый сыщик Шерлок Холмс умело использует дедуктивный метод всякий раз, когда ему приходится разбираться в самых сложных и запутанных ситуациях. Подчеркнем, что в современной науке и практике дедуктивный метод применяется в различных формах, в частности и в виде аксиоматического метода, который в наши дни является мощнейшим и ценнейшим инструментом познания не только в математике, но и во всех её приложениях.
1.4. Пример построения и исследования математической модели Рассмотрим решение задачи: Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 часа. Какова скорость лодки в стоячей воде, если скорость течения реки 3 км/ч. Здесь вместо реального объекта мы имеем дело с текстовой задачей, представляющей содержательную модель этой задачи, на основе которой строим её математическую модель. Пусть
Вот это уравнение и есть математическая модель задачи, возможно и неполная, но отражающая самую существенную связь условий задачи. Конечно, в дальнейшем может возникнуть необходимость дополнить модель неучтёнными ограничениями. Подчеркнём, что в уравнении (1.1) Итак, на первом этапе мы свели решение текстовой задачи к математической задаче решения уравнения (1.1). На втором этапе решаем математическую задачу, т.е. уравнение (1.1) и получаем два корня:
Рисунок 1.2 – Графическое решение уравнения (1.1)
На третьем этапе, имея уже решение математической задачи, необходимо это решение проанализировать, разобраться в его содержательном смысле и сделать правильные выводы. При этом следует иметь в виду, что уравнение (1.1) есть следствие исходной задачи и потому может содержать посторонние решения. Действительно, Теперь очевидно, что при построении математической модели мы не учли ограничение по условию задачи на скорость лодки в стоячей воде:
Если учесть это условие, то из графика (рисунок 1.1) очевидно, что уравнение (1.1) имеет единственное решение. Таким образом, полностью формализованной математической моделью рассматриваемой задачи является смешанная система, состоящая из уравнения (1.1) и неравенства (1.2). Именно эта система является математической записью физических условий, однозначно определяющих скорость лодки в стоячей воде. При решении прикладных задач очень важным является третий этап, заключающийся в обратном переводе результата исследования модели с языка математики на язык прикладной задачи, этап интерпретации (истолкования) результата исследования математической модели, этап, на котором нужно разобраться в решении математической задачи, в реальном смысле этого решения и сделать правильные выводы. Например, широко известный многим ответ «два землекопа и
Математика применяется не непосредственно к реальному объекту, а к его математической модели. А.Д. Мышкис
Поиск по сайту: |
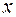 км/ч – скорость лодки в стоячей воде. Тогда скорость лодки по течению
км/ч – скорость лодки в стоячей воде. Тогда скорость лодки по течению  км/ч, а против течения
км/ч, а против течения 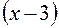 км/ч. По течению реки лодка прошла 25 км за
км/ч. По течению реки лодка прошла 25 км за  ч, а против течения 3 км за
ч, а против течения 3 км за 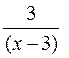 ч. Значит, время, затраченное на весь путь, выраженное через неизвестное
ч. Значит, время, затраченное на весь путь, выраженное через неизвестное 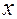 , будет
, будет  ч, но по условию на весь путь затрачено 2 ч. Следовательно,
ч, но по условию на весь путь затрачено 2 ч. Следовательно, . (1.1)
. (1.1)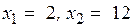 (ответ для модели – это внутримодельное решение). Кстати, это решение легко увидеть на графике функции
(ответ для модели – это внутримодельное решение). Кстати, это решение легко увидеть на графике функции 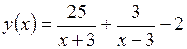 ,построенного с помощью компьютера для
,построенного с помощью компьютера для 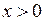 (рисунок 1.1). Этот график пересекает ось абсцисс в двух точках:
(рисунок 1.1). Этот график пересекает ось абсцисс в двух точках:  и
и 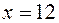 , функция
, функция 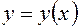 непрерывна и убывает на каждом из двух положительных интервалах оси абсцисс, разделённых точкой
непрерывна и убывает на каждом из двух положительных интервалах оси абсцисс, разделённых точкой 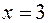 . (Конечно, уравнение (1.1) можно привести к квадратному и решить его обычным способом).
. (Конечно, уравнение (1.1) можно привести к квадратному и решить его обычным способом).
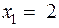 удовлетворяет уравнению (1.1), но не удовлетворяет условию задачи, так как скорость лодки 2 км/ч не может быть меньше скорости течения реки 3 км/ч. Итак, ответ, записанный в терминах исходной задачи: скорость лодки в стоячей воде равна 12 км/ч.
удовлетворяет уравнению (1.1), но не удовлетворяет условию задачи, так как скорость лодки 2 км/ч не может быть меньше скорости течения реки 3 км/ч. Итак, ответ, записанный в терминах исходной задачи: скорость лодки в стоячей воде равна 12 км/ч. . (1.2)
. (1.2) » к школьной задаче из стихотворения С. Я. Маршака, который интерпретирует эти
» к школьной задаче из стихотворения С. Я. Маршака, который интерпретирует эти 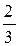 как человека «без ног, без головы», при таком толковании, конечно же, является бессмысленным. Но быть может (условие не приведено), речь шла о числе землекопов, необходимом для выполнения работы за рабочий день? Тогда результат можно истолковать так, что третий землекоп должен был работать
как человека «без ног, без головы», при таком толковании, конечно же, является бессмысленным. Но быть может (условие не приведено), речь шла о числе землекопов, необходимом для выполнения работы за рабочий день? Тогда результат можно истолковать так, что третий землекоп должен был работать 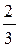 рабочего дня [29, с.128]. При такой интерпретации ответ имеет реальный смысл.
рабочего дня [29, с.128]. При такой интерпретации ответ имеет реальный смысл.