 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Замечания по математической обработке результатов измерений
Процесс измерения состоит из: 1) наблюдений; 2) отсчетов. Задача наблюдений (1) – зафиксировать факт наступления определенного события. Задача (2) – считывание результатов измерений со шкалы прибора. Процесс измерения выражают уравнения измерения (УИ), которые делится на: 1) прямые; 2) косвенные; 3) совместные. Опр.: Если УИ имеет вид Y=CX, (1) то измерения наз. прямыми. Здесь х- отсчет по измерительному прибору в делениях шкалы или отсчет с цифрового табло; с- цена деления шкалы или единичного показания цифрового табло; у – значение измеряемой величины в принятых для нее единицах. Опр.: Измерения наз. косвенными, если УИ имеют вид Z=f(x, y, …, a, b, …), (2) где x, y, … - результаты прямых измерений; a,b, …- физические константы и постоянные приборы; z – значение измеряемой величины в принятых для нее единицах. Пример. Измерение скорости потока в трубопроводе по перепаду давления. Опр.: Измерения наз. совместными, если УИ для этих величин.образуют систему линейно-независимых уравнений. Пример. Для двух измеряемых величин α, β УИ имеют вид: f1(α, β, x1 , y1 , …, а1 , b1 ,, …)=0 ; f2(α ,β, x2 , y2 , …, a2 , b2 , …)=0, где x1 , y1, ..., x2 , y2, ...- результаты прямых или косвенных измерений; а1 , b1, ..., a2 , b2, ...- физические постоянные или постоянные приборов. Измерения одной и той же величины имеют ошибки: прибора, округления, измерений, промахи (грубые ошибки), вычислений. Опр.: Ошибка измерения – разность С понятием ошибки связано понятие точности измерений, чем меньше ошибки, тем выше точность. Задача математической обработки опыта – оценка истинного значения измеряемой величины по получаемым результатам. Иначе, получение приближенного значения μ с возможно меньшей ошибкой. Ошибки включают: 1) грубые; 2) системные (СО); 3) случайные. Так, (1) – возникают из-за нарушения основных условий опыта. В этом случае результат измерений отбрасывают. (2) – ошибка, которая остается постоянной во всей серии измерений. Они влияют на результат. Пример: опыт проводится на приборе с неверной регулировкой; смещением начала отсчета; изменением внешних условий по T и P, которые влияют на результат измерений. Методы устранения СО. 1. Изучение источников ошибок, вызываемых каждым фактором, тарировка прибора на эталонном случае. 2. Устранение источников ошибок: правильная установка прибора, исключающая взаимные влияния. Опр.: Случайная ошибка (СлО) – ошибка, которая изменяется от одного измерения к другому самым неправильным образом и в равной степени может быть как положительной, так и отрицательной. СлО возникает как результат совместного влияния случайных факторов, действия которых незначительны для выделения из общего числа ошибок. Ее рассматривают как суммарный эффект действия таких факторов. СлО являются неустранимыми, их нельзя исключить в каждом из результатов измерений. Для оценки СлО используют аппарат теории вероятности и математической статистики.
1.1. Основные понятия Опр. : Случайной величиной (СВ) наз. переменная, значение которой зависит от случая. СВ бывает: 1) дискретная; 2) непрерывная. Опр.: СВД – это величины, принимающие только отделенные друг от друга значения. Опр. : СВН – это СВ, возможные значения которых непрерывно заполняют некоторый промежуток. СВ ς всегда связана с некоторой функцией f(x) плотности распределения вероятностей СВ. Из теоремы о сложении вероятностей имеем
Опр.: Функция распределения СВ в точке x: F(x) наз. величина
Для СВД также можно определить функцию плотности и функцию распределения. Наиболее полная характеристика СВ дается ее функцией распределения, которая указывает на то, какие значения может принимать СВ и с какими вероятностями. Для обработки СВ в теории вероятности вводятся количественные характеристики: 1) математическое ожидание (среднее значение) М(x).; 2) дисперсия 3) моменты различных порядков. Дадим определения этим понятиям. Пусть x1 , x2, x3, , , xn – возможные значения СВД. P1 , P2, P3, , , Pn – соответствующие им вероятности. Тогда Опр.: Для СВН: Если СВ ς непрерывна и f(x) – ее плотность распределения, то математическим ожиданием (средним значением) для ς наз. интеграл
где μ – результат вычисления интеграла. Опр.: Дисперсия (разброс СВ относительно среднего значения) характеризуется:
где
Опр.: Отклонением стандартным или среднеквадратичным наз. Для сравнения рассеяния различных случайных величин определяют относительное стандартное отклонения Примеры функции плотности распределения – прямоугольное равномерное распределение, нормальное распределение (распределение Гаусса).
1.2. Понятие о выборке Формулировка задача. Предположим: требуется измерить величину l0. Выполнив ряд измерений, имеем набор чисел: x1, x2, x3, … . Какое значение из них следует принять за значение l0? Методика. Из-за влияния ошибок измерения имеем результат измерения СВ – ς, которая имеет некоторую функцию распределения. Если бы эта функция была известна, то можно условиться: принять за l0 одну из характеристик СВ, например, ее среднее значение. Однако на практике возникают ситуации. Функция распределения неизвестна. Поэтому предполагается следующее. Имеет место нормальное распределение, но параметры распределения μ, σ неизвестны. Если возможно производить множество измерений, тогда можно определить функцию плотности и среднее значение. Т.к. число опытов n конечно для ς, то имеем наблюдения: x1, x2, x3, … xn. Эти xi наз. случайной выборкой объема n из возможных значений ς. Из математической статистики имеем: по результатам каждой выборки x1, x2, x3, … xn можно определить величину среднего значения μ и дисперсию σ распределения ς. Тогда, пусть
Выборочная дисперсия СВ:
среднее значение СВ- дисперсия СВ При больших значениях n СВ На этом основывается обстоятельство, что выборочное среднее значение СВ по (1), принимается в качестве оценки значения μ. Кроме того,
Т. е. стандартное отклонение ( Таким образом, при больших n СВ S2 будет как угодно мало отличаться от среднего значения σ2. С учетом сказанного S2 [по (2)] берется в качестве оценки значения σ2. В данном случае для оценки стандартного отклонения величины . Выводы. 1) по формуле (5) вычисляем оценку среднего значения μ (она наз. точечной оценкой). 2) выборочное значение – стандартное отклонение этой оценки – позволяет судить о том, как сильно величина Итак, на данном этапе мы нашли величину μ функции распределения величины Для ее построения используем формулы (1), (5), которые дают доверительный интервал
Здесь kα – положительное число, зависящее от параметра α, где α – коэффициент доверия - вероятность того, что μ заключено внутри интервала (6). Доверительный интервал можно построить, если известны: 1) функция плотности f( Действительно, вероятность
Из (7) для заданного α можно определить
И для коэффициента доверия α имеем интервал для μ
Здесь 1. В случае , если известно, что ς и
Здесь 2. Если функция плотности для СВ
Это означает, что вероятность того, что μ лежит внутри интервала (11), не меньше α, причем γα определяется
Заметим, что в гидродинамических процессах учитывают ошибки: 1) случайные; 2) систематические. Первую группу составляют ситуации их учета: 1) указывается функция плотности; 2) когда систематические ошибки =0, то указывается интервал, в котором с установленной вероятоностью находится случайная ошибка; 3) указывается оценка стандартного отклонения. Функцию плотности f(x) удается указать лишь в немногих случаях, когда она известна, иногда можно определить доверительный интервал. В остальных случаях вычисляется выборочное стандартное отклонение.
1.3. Математическая обработка результатов опыта Завершая эксперимент необходимо выполнить расчеты, провести анализ результатов, сделать выводы. При прямых измерениях получают выборочное среднее
Оценку стандартного отклонения случайных ошибок имеем в виде:
Далее определяем различные системные ошибки
где соответственно приведены ошибки: прибора (определяется по паспорту), округления ( Если известна а – поправка (или систематическая ошибка), то из результата измерений μ= Зам.: 1. Если 2. Если случайные ошибки распределены по нормальному закону, то можно построить доверительные интервалы для коэффициента доверия α. Окончательный результат представляется в виде: 1)
1.4. Косвенные измерения В случае косвенных измерений искомая величина z вычисляется по уравнению z=f(x, y, …, a, b, …), (1) где z- измеряемая величина, x, y, … - результаты прямых измерений, a, b, …- физические постоянные приборов измерений. Для простоты изложения будем иметь Тогда представим
Причем
Разложение (2) предполагает, что для всех
Связь (4) определяет интервал
Чтобы (5) было справедливо, необходимо определить верхнюю границу для СВ ( Рассмотрим случай, когда для результата прямого измерения существенны системные, случайные и приборные ошибки (
Если α<0.8÷0.9, то
где
а различные системные ошибки представляются
Если СлО велики, то
Для проверки (8) имеем 2 случая. 1. (8) не выполнимо. Разложение (2) нельзя применять для оценки 2. (8) работает. Тогда
где Согласно
имеем Для определения возможных ошибок в
Подставляя (10) в (9) и возводя в квадрат, имеем
Пусть
где первое слагаемое отвечает за системные ошибки, второе – за случайные. Таким образом, из (11) с учетом (12), имеем:
Зам.: Соотношение (13) применяется для оценки стандартных отклонений различных систематических ошибок. Для получения оценки стандартного отклонения СлО рассмотрим выражения:
За оценку стандартного отклонения СлО примем:
Кроме того, для случая, если
то (13), (15) преобразуются
Таким образом, полученные формулы (13), (15), (17) позволяют учесть ошибки косвенных измерений, при этом необходима последовательность действий по методике: 1) результаты измерений записываются в таблицу 2) для результатов прямых измерений а) выборочно значение б) выборочное значение стандартных отклонений
3) для каждого аргумента определить а) суммарные системные ошибки
б) интервалы
4) Проверяем условие 5) Вычисляем значение функции
6) вычисляем стандартное отклонение системных и случайных ошибок
7) задаем коэффициент доверия α. Окончательный результат записываем в виде: а) малы; б) Зам.: при совместных измерениях используют метод наименьших квадратов. Пример.
Поиск по сайту: |
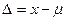 , x – результат измерения, μ- истинное значение.
, x – результат измерения, μ- истинное значение. - вероятность попадания ς в интервал [x0, x1]. Т.к. СВ всегда принимает какое-либо значение, то вероятность того, что наверняка попадем в интервал -[∞, +∞] есть
- вероятность попадания ς в интервал [x0, x1]. Т.к. СВ всегда принимает какое-либо значение, то вероятность того, что наверняка попадем в интервал -[∞, +∞] есть  . Это условие нормировки.
. Это условие нормировки. .
.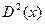 ;
; наз. математическим ожиданием СВ ς, μ – результат суммирования. Если вероятности всех xi равны, то
наз. математическим ожиданием СВ ς, μ – результат суммирования. Если вероятности всех xi равны, то  , где n – число значений x, тогда имеем
, где n – число значений x, тогда имеем  .
. , (1)
, (1) , (2)
, (2) - результат вычисления интеграла;
- результат вычисления интеграла; 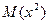 - среднее значение квадрата СВ:
- среднее значение квадрата СВ: .
.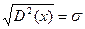 .
. .
.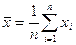 - выборочное среднее значение СВ ς. (1)
- выборочное среднее значение СВ ς. (1) , (2)
, (2) , (3)
, (3) . (4)
. (4) мало отличается от μ
мало отличается от μ ,
,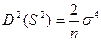 .
. ) при больших объемах выборки может быть как угодно малым.
) при больших объемах выборки может быть как угодно малым. имеем:
имеем: . (5)
. (5) . (6)
. (6) СВ
СВ  . (7)
. (7)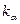 . Кроме того, можем записать
. Кроме того, можем записать . (8)
. (8)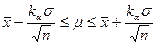 . (9)
. (9) может находиться с заданной достоверностью α, имеет вид
может находиться с заданной достоверностью α, имеет вид . (10)
. (10)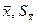 вычисляются по результатам измерений,
вычисляются по результатам измерений, 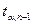 - коэффициент Стьюдента по заданной надежности α и числу измерений n находится по таблицам.
- коэффициент Стьюдента по заданной надежности α и числу измерений n находится по таблицам. . (11)
. (11) .
. . (1)
. (1)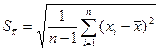 . (2)
. (2) , (3)
, (3) ), субъективных измерений.
), субъективных измерений. , то существенны только случайные ошибки.
, то существенны только случайные ошибки.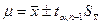 , вероятность P=α; 2)
, вероятность P=α; 2)  : σΣ=…;
: σΣ=…; 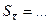 ; n=…. Причем форма 1) работает, когда пренебрегают систематическими ошибками, 2) когда учитываются случайные и систематические ошибки.
; n=…. Причем форма 1) работает, когда пренебрегают систематическими ошибками, 2) когда учитываются случайные и систематические ошибки.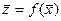 , где
, где  -значение функции от выборочного значения среднего аргумента
-значение функции от выборочного значения среднего аргумента  , (2)
, (2) . (3)
. (3)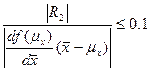 . (4)
. (4) , для которого справедлива (2), т.е.
, для которого справедлива (2), т.е. . (5)
. (5) ), т.е.
), т.е.  .
.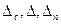 ) :
) : . (6)
. (6) , (7)
, (7) - предельная ошибка прибора, для оценки стандартного отклонения случайных ошибок имеем:
- предельная ошибка прибора, для оценки стандартного отклонения случайных ошибок имеем: будет верхней границей. Если СлО малы, то ими можно пренебречь. Тогда окончательно (5) будет
будет верхней границей. Если СлО малы, то ими можно пренебречь. Тогда окончательно (5) будет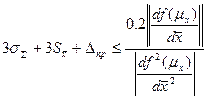 . (8)
. (8) , (9)
, (9) .
. - для левой части (9),
- для левой части (9), - для правой части (9),
- для правой части (9), , т.е. среднее значение функции от выборочного среднего значения аргумента равно искомому значению функции. Поэтому величина
, т.е. среднее значение функции от выборочного среднего значения аргумента равно искомому значению функции. Поэтому величина  при выполнении (2) принимается за оценку μz.
при выполнении (2) принимается за оценку μz. . (10)
. (10)
 . (11)
. (11) , (12)
, (12)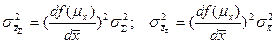 . (13)
. (13) . (14)
. (14) . (15)
. (15) , (16)
, (16) . (17)
. (17) (где i- номер аргумента) функции f надо вычислить
(где i- номер аргумента) функции f надо вычислить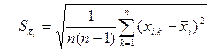

 .
. . Если «да», то действие 5), “нет” – измерения продолжают до тех пор пока условие не будет выполняться.
. Если «да», то действие 5), “нет” – измерения продолжают до тех пор пока условие не будет выполняться.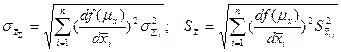 .
. , вероятность P=α, если СлО
, вероятность P=α, если СлО 
 когда учитываются случайные и систематические ошибки.
когда учитываются случайные и систематические ошибки.