 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Квантовый гармонический осциллятор
Более реалистическая модель потенциальной ямы — гармонический осциллятор, потенциальная энергия которого служит параболической функцией координаты (§ 21.6). Модель гармонического осциллятора хорошо описывает колебания атомов внутри молекулы или в кристалле (см. § 10.3, 28.2). Потенциальная энергия гармонического осциллятора
как функция координаты x показана на рис.4. Уравнение Шредингера для одномерного гармонического осциллятора имеет вид
Опустив громоздкие математические преобразования, запишем сразу конечный результат для энергии гармонического осциллятора
т.е. и в этом случае энергия микрочастицы может принимать лишь ряд квантованных, дискретных значений. Минимальное значение энергии гармонического осциллятора
отлично от нуля и называется энергией нулевых колебаний. Если бы минимальная энергия гармонического осциллятора равнялась нулю, то импульс микрочастицы В классической физике было показано (см. § 8.2), что среднее значение энергии теплового движения частицы
Тогда при уменьшении температуры (T→0) среднее значение энергии стремится к нулю, что противоречит квантовомеханическому результату (26). Это противоречие снимается, если предположить, что классическое выражение для энергии теплового движения микрочастиц вблизи абсолютного нуля нарушается, т.е. при понижении температуры энергия колебательного движения микрочастиц (атомов в кристалле) уменьшается не до нуля (как это было бы в случае справедливости классической формулы при T→0), а стремится к некоторому, отличному от нуля значению W=ħω/2 ≠ 0. Этот вывод подтверждается экспериментами по рассеянию света на колебаниях атомов кристалла. При T→0 колебания атомов сохраняются, поэтому даже вблизи абсолютного нуля интенсивность рассеянного света имеет ненулевое значение. Туннельный эффект
Рассмотрим одномерный случай распределения потенциальной энергии по координате x, схематически изображенный на рис. 30.5 (случай потенциальной ступеньки). В области I потенциальная энергия частицы равна нулю и она может свободно перемещаться с некоторой постоянной скоростью и энергией. В области II потенциальная энергия частицы равна Wp. В классической механике показано, что если кинетическая энергия частицы больше высоты потенциальной ступени (Wк>Wp), то частица может переместиться из области I в область II и двигаться дальше в том же направлении (но уже с уменьшенной скоростью и энергией). Если же Wк<Wp, то частица не может проникнуть в область II, а отразится от барьера, изменив направление своего движения на противоположное. Рассмотрим теперь квантовомеханическую трактовку взаимодействии микрочастицы с потенциальной ступенью, ограничиваясь случаем Wк<Wp. Запишем уравнения Шредингера для областей I и II: область I:
область II:
Обозначив
запишем и решим соответствующие характеристические уравнения: для области I:
для области II:
Общие решения уравнений Шредингера имеют вид: для области I:
для области II:
В уравнении (30.28) первое слагаемое описывает падающую волну, связанную с частицей, а второе - отраженную волну. Рассмотрим теперь уравнение (29). Первое слагаемое в нем не удовлетворяет условию конечности, накладываемому на волновую функцию, так как при x →∞ и y2 →∞. Чтобы это условие не нарушалось, необходимо положить А2= 0. Тогда волновая функция (29) принимает вид
а вероятность найтимикрочастицу на некоторой глубине потенциальной ступени
В классической физике вероятность проникновения частицы внутрь потенциальной ступени Wк<Wp равна нулю, так как в этом случае ее кинетическая энергия становится отрицательной. Однако в квантово-механической трактовке такой процесс становится возможным.
Рассмотрим теперь одномерный случай распределения потенциальной энергии, доказанный на рис. 30.6. Участок II, в пределах которого величина потенциальной анергии больше, чем в окружающих его областях I и III, называетсяпотенциальным барьером. Пусть слева к потенциальному барьеру подлетает микрочастица с энергией Wк<Wp. Согласно изложенному эта микрочастица может проникнуть в глубь потенциального барьера и оказаться на его правой границе с вероятностью
где d — ширина барьера. Оказавшись на правом краю барьера, частица становится свободной и может двигаться дальше в прежнем направлении с той же скоростью и энергией, которые она имела, подлетая к барьеру. Явление прохождения микрочастицы через потенциальный барьер в случае, если ее энергия меньше,чем высота барьера, носит название туннельного эффекта. Согласно (30.31) прозрачность барьера D ,т.е. вероятность прохождения микрочастицы через потенциальный барьер, определяется выражением
Выражение (30.32) справедливо для потенциального барьера простейшей прямоугольной формы, а для барьера произвольной формы (рис. 7) прозрачность определяется формулой
Из формул (32) и (33) видно, что вероятность прохождения микрочастицы через потенциальный барьер увеличивается по мере уменьшения ширины барьера и возрастания энергии частицы. Рассмотрим примеры некоторых физических явлений, которые описываются закономерностями туннельного эффекта. 1. Если два проводника разделены слоем диэлектрика, то ток через такой контакт протекать не может, однако при малой толщине диэлектрической прослойки (d≤10-8м) электроны могут переходить сквозь слой диэлектрика, создавая туннельный контакт. Наиболее интересен тот случай, когда оба металла находятся в сверхпроводящем состоянии (см. § 34.2). 2. На границе между полупроводниками с электронным и дырочным типами проводимости образуется контактная разность потенциалов, создающая потенциальный барьер для перехода электронов. При определенных условиях формирования контакта становятся возможными туннельные переходы электронов через него (туннельный диод — см. § 33.7). 3. На основе туннельного эффекта создан электронный микроскоп принципиально нового типа. В этом микроскопе тончайшее металлическое острие приближается к исследуемой поверхности на малое расстояние и фиксируется туннельный электрический ток, протекающий через разрядный промежуток. При перемещении острия мельчайшие неровности на исследуемой поверхности изменяют ширину потенциального барьера и, следовательно, значение силы тока в цепи. Прибор настолько чувствителен, что позволяет фиксировать отдельные атомы.
Лекція 42. Квантово-механiчна модель атома водню. Дослiд Штерна i Герлаха. Спiн електрона. Принцип Паулi. Перiодична система елементiв.
Поиск по сайту: |

 Рис. 4
Рис. 4



 также равнялся бы нулю. Это возможно лишь в том случае, когда частица находится в положении равновесия, т.е. ее координата x=0. Однако высказанное предположение (Wo=0) противоречит соотношению неопределенностей Гейзенберга, поскольку при этом допускается возможность одновременного точного определения координаты (x=0) и импульса микрочастицы (p=0), что невозможно.
также равнялся бы нулю. Это возможно лишь в том случае, когда частица находится в положении равновесия, т.е. ее координата x=0. Однако высказанное предположение (Wo=0) противоречит соотношению неопределенностей Гейзенберга, поскольку при этом допускается возможность одновременного точного определения координаты (x=0) и импульса микрочастицы (p=0), что невозможно.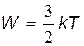
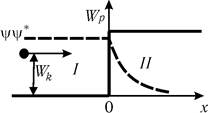 Рис. 5
Рис. 5










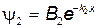 .
.

 Рис. 6
Рис. 6
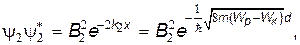


 Рис. 7
Рис. 7