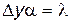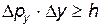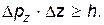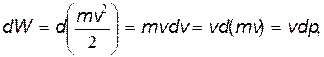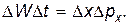Соотношение неопределенностей Гейзенберга

В классической механике состояние движения частицы в любой момент времени можно определить, задав значения ее координат и импульса. Эти значения находятся из решения соответствующих уравнений движения, основанных на законах Ньютона. В случае же описания волновых процессов в классической механике применяется иная схема представлений, основанная на понятиях механики сплошных сред. При этом характеристики, описывающиемеханическое движение и волновые процессы несовместимы между собой.

Как было указано, микрочастицы одновременно обладают как волновыми, так и корпускулярными свойствами, поэтому их движение не может быть описано в рамках чисто корпускулярных или чисто волновых представлений. Однако, если мы попытаемся (хотя бы приближенно) описать движение микрочастицы как корпускулы (т.е. по определенной траектории), то наличие у нее волновых свойств должно привести при таком описании к появлению некоторых ограничений. Такие ограничения были установлены в 1927 г. В. Гейзенбергом и носят название соотношений неопределенности.

Для нахождения этих соотношений рассмотрим мысленный опыт по одновременному определению координаты и импульса микрочастицы (например, электрона) — рис. 30.1. Пусть микрочастица движется в положительном направлении оси x и имеет импульс p=p_x. Для того чтобы определить координату микрочастицы по оси y, поставим на ее пути экран с узкой прямой щелью шириной а. Если частица пройдет через щель, то ее координата y будет определена с точностью до ширины щели, т.е. Δy=a. Однако после прохождения щели микрочастица вследствие волновых свойств дифрагирует и отклоняется от своего первоначального направления движения вверх или вниз, т.е. получает неопределенный по величине дополнительный импульс Δp_y. При пропускании через щель значительного числа частиц на экране возникает дифракционная картина чередующихся максимумов и минимумов, центральная часть которой схематически показана на рис. 30.1, Ограничимся в дальнейшем рассмотрением центральной, наиболее интенсивной части дифракционной картины, заключенной между первыми дифракционными минимумами, которые соответствуют отклонению микрочастиц на угол a от первоначального направления.

Рис. 1

С корпускулярной точки зрения отклонение микрочастицы от первоначального направления на угол a можно объяснить тем, что при прохождении щели она получает дополнительный импульс

(2)

С волновой точки зрения дифракция электронов объясняется так же, как и дифракция света. Направление на первый дифракционный минимум можно найти из условия

(3)

С корпускулярно-волновой точки зрения соотношения (2) и (3) должны рассматриваться совместно. Для этого исключим из них формул уголaи подставим значение l из формулы де Бройля, которая учитывает наличие как волновых, так и корпускулярных свойств у микрочастиц. Имеем

(4)

Смысл этого соотношения состоит в том, что невозможно одновременно сколь угодно точно определить координату и импульс микрочастицы.

Устремление Δy нулю приводит к тому, что мы теряем всякое представление о значении импульса микрочастицы, поскольку разброс его возможных значений Δp_y=h/Δy→∞. И наоборот, если мы попытаемся точно измерить импульс микрочастицы (Δp_y→0) то ее положение в пространстве становится совершенно неопределенным, так как Δy=h/ΔΔp_y→∞.

При выводе соотношения неопределенности (4) был учтен только центральный дифракционный максимум. С учетом максимумов более высокого порядка можно записать:

(5)

Аналогичные соотношения можно получить и для других пространственных координат и проекций импульса:

	(6)

Соотношения неопределенностей не связаны с несовершенством методов измерения или измерительных приборов. Эти соотношения получены при попытке описания движения микрочастицы с помощью классических характеристик (координаты и импульса), в то время как микрочастица имеет также волновые свойства. Поскольку в классической физике принимается, что измерение координаты и импульса частицы может быть проведено с любой точностью, то соотношение неопределенностей указывает границы применения классического способа описания движения микрообъектов.

Если представить неопределенность импульса как ∆p_x=m∆v_x , то

Отсюда следует, что для макроскопических объектов с большими массами произведение ∆x∆v_x очень мало, близко к нулю. Это означает, что при описании движения макротел в классической физике можно пользоваться понятием траектории, поскольку положение макрообъекта и его скорость можно определить с очень высокой точностью. Например, при локации Луны с помощью лазерных импульсов расстояние до ее поверхности было определено с точностью до ∆x ~1 м. Это очень высокая точность, если учесть, что расстояние до Луны R ~ 10⁸ м. Неопределенность в измерении скорости Луны при этом будет

что лежит за пределами возможностей современных измерений. Отсюда ясно, что в данном случае можно пользоваться классическим описанием движения Луны как движения по строго определенной траектории.

Рассмотрим теперь движение микрочастицы — электрона в атоме водорода. Координату движущегося электрона можно определить с точностью до размеров атома ∆x ~10^{-10 м и тогда} ∆v_x =h/m∆x=7,3∙106 м/с, что в несколько раз превышает значение скорости электрона, вычисленной по теории Бора — v=2,3∙106 м/с. Очевидно, что в данном случае понятие траектории теряет смысл, т.е. при описании движения электрона в атоме законы классической механики неприменимы.

Корпускулярно–волновой дуализм микрочастиц приводит к тому, что при их описании возникает неопределенность не только в координатах и импульсах, но и в значенияхих энергии. Действительно, изменение кинетической энергии

или

Отсюда

Поскольку ∆x∆p_x≥h, то

Соотношение (7) показывает, что если частица находится в нестационарном состоянии (например, атом в возбужденном состоянии) в течение времени ∆t, то значение ее энергии может быть задано с ограниченной точностью. Из выражения (7) следует, что частота излученного фотона также должна иметь неопределенность ∆n =∆W/h, т.е. линии спектра охватывают интервал частот от n–∆n до n+∆n. Опыт действительно показывает, что излучение атомов, возникающее в результате переходов электрона с одной стационарной орбиты на другую , не является строго монохроматичным.

Поиск по сайту: