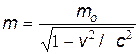|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Энергия и импульс световых квантовСтр 1 из 26Следующая ⇒
Й семестр «Квантовое ядро» Лекція 37. Корпускулярно-хвильова природа свiтлового випромiнювання. Проблеми випромiнювання абсолютно чорного тiла. Гiпотеза Планка. Пiрометрiя. КОРПУСКУЛЯРНО-ВОЛНОВАЯ ПРИРОДА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ Проблемы излучения абсолютно черного тела Основные определения Электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств тела, называется тепловым излучением. Тепловое излучение является равновесным. Поместим в замкнутую адиабатическую оболочку несколько тел с различными температурами. В соответствии со вторым началом термодинамики в такой системе начнут протекать процессы, которые приведут к выравниванию температур тел. Эти процессы состоят в испускании и поглощении электромагнитного излучения телами, находящимися внутри полостей не прекращаются после достижения термодинамического равновесия. Это может быть лишь в том случае, если между телом и излучением устанавливается равновесие: сколько энергии излучает тело, столько же ее оно и поглощает. Введем некоторые количественные характеристики теплового излучения. Испускательной способностью тела называется количество энергии, испускаемой за единицу времени с единицы площади в единичном интервале частот:
Спектральной плотностью излучения называется количество энергии электромагнитного излучения, приходящегося на единичный интервал частот и сосредоточенного в единичном объеме:
Поскольку тепловое излучение является равновесным, то между испускательной способностью тела и спектральной плотностью излучения должна существовать пропорциональная зависимость r(n,T)~u(n,T). Для абсолютно черного тела эта зависимость имеет вид
Интегральной испускательной способностью (энергетической светимостью) называется количество энергии, испускаемой за единицу времени с единицы площади во всем интервале частот от 0 до ∞. Между интегральной испускательной способностью Rэ(Т) и испускательной способностью r(n,T) существует связь.
Поглощательной способностью тела называется отношение поглощенной энергии ко всей падающей на тело энергии в интервале частот от n до n+dn:
Абсолютно черным телом (АЧТ) называется такое тело, поглощательная способность которого для всех частот и температур равна единице: a(n,T)=1. Моделью АЧТ может служить небольшое отверстие, вырезанное в полой сфереиз непрозрачного вещества (рис. 1). Луч света, попадая через такое отверстие внутрь полости, испытывает многократные отражения и практически полностью поглощается.
Серым называется такое тело, поглощательная способность которого меньше единицы, но постоянна для всех частот и температур (рис.2). У цветного тела поглощательная способность является функцией частоты и температуры. Закон Кирхгофа Кирхгоф установил закон, согласно которому отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и является универсальной функцией от частоты и температуры:
Для АЧТ поглощательная способность равна единице, поэтому для такого тела испускательная способность совпадает с универсальной функцией
Пусть адиабатическая полость, внутренние стенки которой являются АЧТ, заполнена равновесным тепловым излучением. Выделим на поверхности полости участок площадью dS и подсчитаем для него баланс энергии. С этого участка излучается энергия r*(n,T)dS, где r*(n,T) — испускательная способность АЧТ. Для сохранения термодинамического равновесия столько же энергии должно поглощаться.. Поскольку для АЧТ a(n,T) = 1, то со стороны других участков на выделенный должна падать энергия, равная r*(n,T)dS. Заменим теперь выделенный участок стенки полости некоторым произвольным телом, у которого испускательная способность равна ri(n,T), а поглощательная аi(n,T)<1. Составим теперь баланс энергии для этого случая. Как и в первом случае, на этот участок будет падать энергия r*(n,T)dS, часть которой аi(n,T)r*(n,T)dS, будет поглощаться; излучаться же будет энергия, равная ri(n,T). Поскольку процесс равновесный, то
откуда
Формула (29.7) справедлива для любого тела — тем самым закон Кирхгофа доказан. Законы излучения АЧТ
Основная проблема изучения АЧТ - определение вида функции r*(n,T). Эксперименты позволили найти эту зависимость и сформулировать некоторые частные законы излучения АЧТ. Экспериментальные зависимости r*(n,T) для двух значений температуры показаны на рис. 3. Видно, что излучательная способность АЧТ падает при малых и больших частотах и достигает максимума при некотором значении nm. С ростом температуры излучательная способность возрастает, а ее максимальное значение смещается в область больших частот. Сформулируем частные законы излучения АЧТ. 1. Закон Стефана - Больцмана. Интегральная испускательная способность АЧТ пропорциональна четвертой степени его абсолютной температуры, т.е.
где s — постоянная Стефана - Больцмана. 2. Закон смещения (Вина). Частота, на которую приходится максимум испускательной способности АЧТ, пропорциональна его абсолютной температуре:
где b — постоянная Вина. Закон Вина устанавливает положение максимума кривой r*(n,T) с повышением температуры максимум смещается в область более высоких частот. 3. Высота максимума кривой r*(n,T). Она устанавливается следующим законом (иногда его называют вторым законом Вина): максимальная испускательная способность АЧТ пропорциональна кубу его абсолютной температуры:
где с — постоянная. Эти законы, однако, не дают возможности воспроизвести явный вид функции r*(n,T). Для нахождения вида этой функции Д. Релей и Д. Джине воспользовались классическим законом распределения энергии по степеням свободы (§ 9.3) и получили следующее выражение для испускательной способности АЧТ:
где c — скорость света; k — постоянная Больцмана. Формула Релея – Джинса (11) хорошо согласуется с опытом в области малых частот, однако в области больших частот эта формула резко расходится с экспериментом (пунктирная линия на рис. 3). Такое несоответствие теории и эксперимента получило название ультрафиолетовой катастрофы. Таким образом, в рамках классической физики не удалось объяснить закономерности теплового излучения АЧТ. Причина этого состоит в принципиальной неприменимости законов классической физики к элементарным процессам, обусловливающим тепловое излучение. 4. Формула Планка. В 1900 г. М. Планк высказал гипотезу, что процесс испускания и поглощения света происходит не непрерывно, а определенными порциями (квантами), энергия которых определяется формулой
где h = 6,62·10-34 Дж·с — универсальная константа, называемая постоянной Планка. С помощью таких квантовых представлений о природе излучения Планк нашел функцию распределения энергии излучения АЧТ по частотаv (см. прил. 6):
которая очень точно воспроизводит экспериментальную кривую r*(n,T). С помощью формулы Планка (29.13) можно объяснить все закономерности излучения АЧТ, установленные ранее. В частности, в области низких частот, когда hn/kT<<1, можно приближенно представить экспоненту в (29.13) в виде
Подставив (14) в (13), получим формулу Релея – Джинса. Закон Стефана – Больцмана можно получить из формулы Планка, проинтегрировав выражение (13) по частоте в пределах от 0 до ∞:
Для вычисления интеграла сделаем замену hn/kT=x; отсюда n=kTx/h, dn=kTdx/h. Тогда
Мы получили закон Стефана – Больцмана, причем постоянная
Закон смещения Вина можно получитьиз формулы Планка, приравняв первую производную по частоте к нулю:
Взяв производную, получим
где
Полученное уравнение решается методом последовательных приближений и имеет единственный корень x = 2,821. Из формулы (15) следует
т.е. мы получили закон Вина с постоянной b;
И наконец, второй закон Вина получим, если подставим (16) в формулу Планка:
5. Пирометрия. Раздел технических приложений, использующих закономерности теплового излучения для измерения температуры нагретых тел, называется пирометрией. Пирометры — это приборы для измерения температуры нагретых тел по интенсивности их теплового излучения. Основное условие применимости методов пирометрии состоит в том, что тело, температуру которого измеряют с помощью пирометра, должно находиться в тепловом равновесии и обладать поглощательной способностью, близкой к единице. Различают яркостные, цветовые и радиационные пирометры. В простейшем визуальном яркостном пирометре с исчезающей нитью объектив фокусирует изображение исследуемого тела на плоскость, в которой расположена нить (ленточка) специальной лампы накаливания. Через окуляр и красный фильтр нить рассматривают на фоне изображения тела и, изменяя ток накала нити, добиваются, чтобы яркости нити и тела были одинаковы (нить становится неразличимой на фоне тела). Шкалу прибора, регистрирующего ток накала, градуируют обычно в градусах Цельсия или Кельвина, и в момент выравнивания яркостей нити и тела прибор показывает так называемую яркостную температуру тела Tя. Для измерения температуры тел, которые в оптическом диапазоне являются серыми, применяют цветовые пирометры. Этими пирометрами измеряют яркость тела в двух областях спектра — синей и красной (например, lc = 0,48 мкм и lкр= 0,60 мкм). Шкала прибора градуирована в °С и показывает цветовую температуру Tц. Наиболее чувствительны радиационные пирометры, регистрирующие суммарное излучение тела. Действиеих основано на законах Стефана –Больцмана и Кирхгофа. Объектив радиационного пирометра фокусирует наблюдаемое излучение на приемник, сигнал от которого регистрируется прибором, калиброванным по излучению АЧТ и показывающим радиационную температуру Tр. В качестве приемника используют либо термостолбик (батарею последовательно соединенных термопар), либо болометр, действие которого основано на уменьшении сопротивления полупроводников при их нагреве. Измеряемые с помощью пирометров температуры (яркостная Tя, цветовая Tц, или радиационная Tр) пересчитываются на основании законов теплового излучения в истинную. Например, истинная T и радиационная Tр температуры связаны соотношением
где aT — поглощательная способность тела. Методами пирометрии измеряют температуру в печах и других нагревательных установках, температуру расплавленных металлов, нагретых газов, племени, плазмы. Их широко используют в автоматизированных системах контроля и управления температурными режимами разнообразных технологических процессов.
Лекція 38. Зовнiшнiй фотоефект. Енергiя i iмпульс свiтлових квантiв. Ефект Комптона. Свiтловий тиск. Внешний фотоэффект Явление взаимодействия электромагнитного излучения с веществом, при котором энергия передается непосредственно электронам вещества, и они выходят в окружающее пространство, называется внешним фотоэффектом. Экспериментально были установлены следующие закономерности фотоэффекта: 1) максимальная энергия фотоэлектронов не зависит от интенсивности света; 2) максимальная энергия фотоэлектронов пропорциональна частоте падающего света; З) число фотоэлектронов пропорционально интенсивности света; 4) существует некоторое пороговое значение частоты n0 которое называется красной границей фотоэффекта – при частоте света n<n0 фотоэффект прекращается; 5) фотоэффект практически безынерционен. Эти закономерности не могли быть объяснены с точки зрения волновой природой света. По этой теории энергия фотоэлектронов должна быть пропорциональна интенсивности падающего света, а красной границы вообще не должно было существовать. Правильная теория фотоэффекта была дана А. Эйнштейном (1905 г.), который исходил из корпускулярных представлений о природе света. Согласно А. Эйнштейну явление фотоэффекта представляет собой неупругое соударение кванта света (фотона) с одним из электронов вещества, в результате которого электрон, получивший избыточную энергию, может выйти за пределы вещества. Закон сохранения энергии в этом процессе описывается уравнением Эйнштейна.
где hn — энергия фотона; А — работа выхода электрона из вещества. Из уравнения (17) видно, что mv2/2 ~ n, тем самым объясняется вторая закономерность фотоэффекта. Существование красной границы фотоэффекта объясняется тем, что по мере уменьшения частоты падающего света уменьшается также кинетическая энергия электронов и при некоторой частоте n=n0 mv2/2=0 фотоэффект прекращается. Пороговою частоту n0 можно найти из условия hn0=A откуда,
Интенсивность света определяется соотношением I=Nhn где N— число квантов света и поэтому с ростом интенсивности света возрастает число актов взаимодействия фотонов с электронами (и растет число вылетевших электронов (но не их энергия). Этим объясняется первая и третья закономерноcти фотоэффекта. Уравнение (17) описывает так называемый однофотонный фотоэффект, когда электроном поглощается лишь один фотон (вероятность одновременного поглощения электроном двух и более фотонов ничтожно мала). В связи с созданием мощных источников монохроматического излучения (лазеров), был обнаружен многофотонный фотоэффект. В этом случае электрон может одновременно поглотить не один, а несколько фотонов. Уравнение Эйнштейна для многофотонного фотоэффекта принимает вид
При этом пороговая частота сдвигается в область малых частот.
Явление внешнего фотоэффекта находит широкое применение в технике для преобразования световых сигналов в электрические с последующей их обработкой. Рассмотрим основные типы фотоэлектрических приборов, использующих внешний фотоэффект. 1. Вакуумные фотоэлементы — это фотокатод (чаще всего из щелочного металла) и анод, помещенные в прозрачную колбу, в которой создается высокий вакуум. Преимущества этих фотоэлементов следующие: строгая пропорциональность между силой фототока и световым потоком; малая инерционность (t~10-9…10-10 с); отсутствие усталостных явлений; высокое внутреннее сопротивление. Основной недостаток — невысокая чувствительность ~1…10 мкА/лм. Область применения — точные измерения световых потоков в лабораторных условиях. 2. Газонаполненные фотоэлементы отличаются от вакуумных тем, чтоих баллов заполняется инертным газом при невысоком давлении (P»0,1…1 Па). При прохождении через газ фотоэлектронов последние ионизируют его молекулы, что приводит к возрастанию тока и несколько более высокой чувствительности ~10…100 мкА/лм. Газонаполненные фотоэлементы также обладают строгой пропорциональностью между световым потоком и силой тока, а их инерционность (t~10-9…10-10 с) достаточна для большинства практических применений. Вследствие протекания необратимых процессов адсорбции газа-наполнителя стабильность их работы несколько ниже, чем у вакуумных фотоэлементов. 3 Рис. 4 3. Фотоэлектронные умножители (рис. 4). В этих приборах для усиления фототока используется явление вторичной электроннойэмиссии, которое состоит в выбивании из металла вторичных электронов при его бомбардировке ускоренными электронами. При попадании света на фотокатод К из него выбиваются электроны, которые ускоряются электрическим полем при движении к электроду Э1, заряженному положительно, и выбивают из него вторичные электроны. Далее этот процесс повторяется на следующих электродах Э2-ЭN и в результате в цепи анода возникает значительный ток. Чувствительность фотоумножителей весьма велика и составляет 0,1...1 А/лм. Их недостатки: сложность конструкции и необходимость использования высоких напряжений (U ~ 1…1,5 кВ). Область применения — регистрация очень слабых световых потоков. Энергия и импульс световых квантов По современным представлениям световой квант отождествляется с элементарной частицей — фотоном, который существует, лишь двигаясь со скоростью света. Как и всякий материальный объект, фотон обладает энергией, которая связана с его массой соотношением Эйнштейна (21). Энергию фотона можно также найти по формуле Планка (12). Приравнивая (21) к (12), находим массу фотона
Следует отметить, что поскольку фотон существует лишь двигаясь со скоростью света, его масса покоя равна нулю: m0 = 0. Фотон обладает импульсом, величина которого определяется формулой
или с учетом того, что n=c/l,
Эффект Комптона Наиболее наглядное представление о фотоне как частице проявляется в эффекте Комптона, который состоит в том, что при взаимодействии фотона со свободным (или слабо связанным с атомом) электроном фотон отдает часть своей энергии электрону. При этом получается рассеянный фотон, импульс которого составляет угол q с направлением первоначального двоения. Свои опыты А. Комптон проводил в 1923 г., изучая прохождение монохроматических рентгеновских лучей через вещество. Как показали опыты, рассеяние рентгеновских лучей происходит с изменением их длины волны, независящим от природы рассеивающего вещества и определяющимся только углом рассеяния. Этими особенностями комптоновское рассеяние принципиально отличается от классического (рэлеевского) рассеяния, которое, как известно, происходит без изменения длины волны. Все особенности эффекта Комптона можно объяснить в рамках квантовой теории, рассматривающей процесс взаимодействия фотона со свободными электронами как упругое соударение. На рис. 5 показана импульсная диаграмма взаимодействия фотона и электрона. Предположим, что до соударения с фотоном электрон покоился, так что его импульс p=mv =0, а энергия равна энергии покоя W0=m0c2. Применим к рассматриваемому процессу законы сохранения импульса и энергии:
Здесь
а его импульс p=mv. В уравнениях (21) применены релятивистские выражения для энергии и импульса электрона, поскольку рентгеновские фотоны, которые использовались в опытах Комптона, сообщали электронам релятивистские скорости. Опуская громоздкие математические выкладки, напишем сразу конечный результат, который следует из (21):
Здесь Dl=l¢-l — изменение длины волны фотона при его рассеянии на электроне на угол q. Величина L=h/m0c называется комптоновской длиной волны электрона. Из (22) видно, что максимальное изменение длины волны фотона наблюдается при его рассеянии назад (q=180о). В этом случае фотон отдает электрону максимально возможную часть своей энергии. Результаты измерений Комптона находятся в полном соответствии с формулой (22). Лекція 39. Модель атома Бора-Резерфорда.
Поиск по сайту: |
 .
.
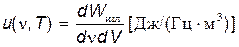 .
.

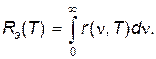
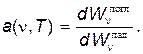
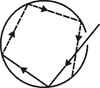 Рис.1.
Рис.1.
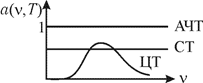 Рис. 2.
Рис. 2.
 .
.
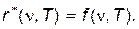
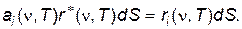

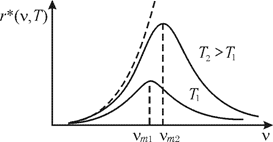 Рис. 3
Рис. 3
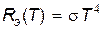 .
.
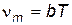 ,
,
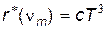
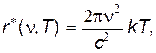
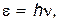
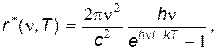
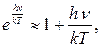

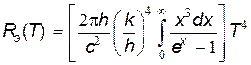



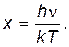
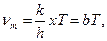
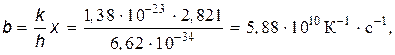
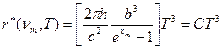
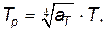
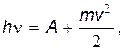
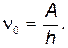

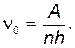
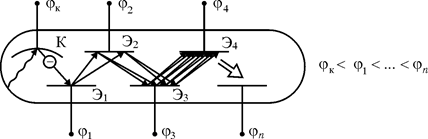
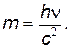
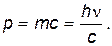


 Рис. 5
Рис. 5
 и
и 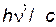 — импульсы фотона до и после взаимодействия с электроном. После соударения с фотоном энергия электрона становится равнойmc2, где масса движущегося электрона
— импульсы фотона до и после взаимодействия с электроном. После соударения с фотоном энергия электрона становится равнойmc2, где масса движущегося электрона