 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Принцип Паули. Периодическая система элементов Менделеева
Состояние электрона в атоме определяется с помощью четырех квантовых чисел n, l, m, s. Физические величины, определяемые этими числами, и возможные их значения приведены в табл. 31.1. Таблица 31.1
В 1925 г. В._Паули установил принцип: в любом атоме не может быть двух электронов с одинаковым набором квантовых чисел, т.е. электроны должны отличаться друг от друга хотя бы одним квантовым числом. Пользуясь принципом Паули, можно найти максимальное число электронов с одинаковым значением главного квантового числа и отличающихся друг от друга хотя бы одним квантовым числом l, m, s. Различные состояния атома, характеризующиеся значением главного квантового числа n=1 и n=2, приведены в табл. 31.2. Видно, что максимальное число электронов, находящихся в состоянии с n=1, равно двум, а при n=2 это число равно восьми. В общем случае максимальное число электронов, которые находятся в состоянии со значением главного квантового числа n, равно 2n2. Электроны с одинаковым значением главного квантового числа образуют оболочки, которые обозначаются буквами K (n=1), L (n=2), M (n=3) и т.д. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим значению орбитального квантового числа l. Число подоболочек равно порядковому номеру n оболочки. Максимальное число электронов в подоболочке с данным l равно 2(2l+1). В порядке возрастания орбитального квантового числа l=0, 1, 2, 3, 4, ... подоболочки обозначаются буквами соответственно s, p, d, e, f. Таблица 31.2
Теоретическое обоснование периодической системы элементов Менделеева основано на трех положениях. 1. Общее число электронов в атоме данного элемента равно его порядковому номеру в таблице Менделеева. Это означает, что суммарный отрицательный заряд электронов компенсирует положительный заряд ядра и поэтому атом в целом электронейтрален. 2. При заполнении электронных оболочек должен выполняться принцип минимума энергии, который состоит в том, что при переходе от одного элемента к другому, т.е. при присоединении к атому нового электрона, в первую очередь заполняются состояния с наименьшей энергией. 3. Заполнение электронами энергетических состояний в атоме происходит в соответствии с принципом Паули. Исходя из этих принципов, рассмотрим теперь строение начальных периодов таблицы Менделеева. Первый период содержит два элемента — водород и гелий. В атоме водорода имеется один электрон, который заполняет состояние с квантовыми числами n=1, l=0, m=0, s=+1/2 или –1/2. В атоме гелия два электрона имеют одинаковые числа n=1, l=0, m=0, но разные значения спиновых квантовых чисел: для одного из них s=+1/2, а для другого s=–1/2. Эти два электрона полностью заполняют наинизшую K-оболочку. Второй период начинается с атома лития, который имеет три электрона: два из них образуют K-оболочку, а третий находится на L-оболочке, соответствующей значению главного квантового числа n=2. Следующие далее по мере возрастания номеров элементы Be, B, C, N, O, F, Ne также имеют полностью заполненную K-оболочку, а остальные электроны заполняют L-оболочку, причем сначала заполняется подоболочка s (Li, Be), а затем подоболочка p — остальные элементы второго периода. Заполнение p-оболочки заканчивается на атоме неона и им же завершается второй период периодической системы. C третьего периода, т.е. со щелочного элемента натрия, начинается заполнение M-оболочки (n=3): сначала заполняется s-подоболочка (Na, Mg), а затем p-подоболочка. Заканчивается период инертным газом аргоном, у которого p-подоболочка полностью заполнена. В соответствии с принципом минимума энергии оболочки должны быть последовательно заполнены одна за другой, а в пределах каждой оболочки - сначала s-подоболочка, затем p-, d-, f-подоболочки. Однако, начиная с четвертого периода такой порядок нарушается: сначала заполняется более высокая подоболочка, а затем более низкая. Как показывают строгие квантово-механические расчеты, это связано с тем, что энергия электрона зависит не только от главного квантового числа, но и от орбитального. Поэтому энергетически более выгодным может оказаться состояние с большим n, но меньшим l. Группу элементов от лантана (La57) до лютеция (Lu71) называют лантаноидами или редкоземельными элементами. У них происходит заполнение внутренних оболочек при практически неизменных внешних оболочках, поэтому лантаноиды характеризуются близкими химическими свойствами, подобным образом ведут себя актиноиды — группа элементов от актиния (Ac89) до лоуренсия (Lr103) в седьмом периоде.
Лекція 43. Рентгенiвськi спектри. Молекулярнi спектри. Комбiнацiйне розсiювання свiтла. Люмiнесценцiя. Рентгеновские спектры Рентгеновские лучи — это элекромагнитные волны с малой длиной волны — l £ 0,1 нм. Рентгеновское излучение возникает при бомбардировке электронами электрода, выполненного из материала, состоящего из атомов с z > 20. Различают сплошной и характеристический (линейчатый) рентгеновские спектры.
Сплошной рентгеновский спектр (рис. 31.3) возникает при сравнительно низком ускоряющем напряжении в рентгеновских трубках (U ≈ (3…5)×104 В). Форма сплошного рентгеновского спектра напоминает спектр излучения АЧТ (см. § 29.1), но роль температуры играет ускоряющее напряжение. принципиальное различие этих двух типов спектров состоит в том, что спектр сплошного рентгеновского излучения ограничен со стороны коротких волн значением l0, при котором интенсивность излучения обращается в нуль. С ростом напряжения значение коротковолновой границы l0 смещается в область коротких волн. Происхождение сплошного спектра, существование в нем коротковолновой границы и ее зависимость от напряжения можно объяснить следующим образом. При столкновении с анодом электрон испытывает резкое торможение, т.е. движется с большим отрицательным ускорением. В соответствии с законами классической электродинамики ускоренно движущийся заряд излучает электромагнитные волны. Строгие расчеты по теории Максвелла позволили найти аналитическое выражение для зависимости I(l), показанной на рис. 31.3. Для пояснения существования коротковолновой границы сплошного спектра запишем закон сохранения энергии для взаимодействия электрона с анодом. Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию mv2/2=eU, которая частично расходуется на излучение светового кванта с энергией hn, а частично преобразуется в тепловую энергию, приводящую к разогреву анода: eU=hn+Q. Для каждого из электронов, соударяющихся с анодом, соотношение между hn и Q разное: чем больше Q, тем меньше hn, и наоборот. Поэтому рентгеновский спектр является сплошным. В некоторых благоприятных случаях вся кинетическая энергия электрона переходит в энергию электромагнитного излучения: eU= hn. Поскольку n0=c/l0, то из последнего соотношения следует
Таким образом, с ростом напряжения l0 уменьшается, что согласуется с опытом (рис. 31.3).
При более высоких напряжениях рентгеновский спектр радикально преобразуется: на фоне сплошного рентгеновского спектра появляются острые пики, совокупность которых образует линейчатый спектр. Механизм возникновения линейчатого спектра следующий. При высоких напряжениях энергия электрона становится достаточной для того, чтобы выбить электрон с одной из внутренних оболочек атома. При этом на внутренней оболочке возникает незаполненное место - вакансия, которая далее может быть заполнена в результате перехода электрона с более высокой оболочки. Такой переход будет сопровождаться излучением рентгеновского кванта определенной частоты. Если вакансия образовалась на K-оболочке, то переходы типа L→K,. M→K, N→K приводят к образованию в рентгеновских спектрах K-серии (рис. 31.4). L-серия возникает в результате переходов электрона с более высоких оболочек на L-оболочку: M→L, N→L и т.д. Аналогичным образом возникают и другие серии линейчатого рентгеновского спектра. Экспериментально было установлено, что линии какой-либо серии удовлетворяют соотношению, напоминающему обобщенную формулу Бальмера для водородоподобных атомов (см. § 29.6):
где R — постоянная Ридберга; s— постоянная экранирования; n и m — натуральные числа, причем n < m. Формула (31.6) носит название закона Мозли. Смысл постоянной экранирования состоит в том, что электрон, осуществляющий переход на более низкую оболочку, «чувствует» не весь заряд ядра ze, а заряд (z – s)e, ослабленный экранирующим воздействием других электронов. Например, для перехода L→K s=1, так как на K-оболочке остается один электрон, уменьшающий заряд ядра на величину одного элементарного заряда. Частота первой линии K-серии, возникающей в результате перехода L→K, находится по формуле
Формула (31.7) позволила наиболее точно определить заряд ядра атома и сыграла выдающуюся роль в обосновании ядерной модели атома. Необходимо отметить, что поскольку линейчатый рентгеновский спектр возникает при переходах электронов на внутренних оболочках атома, то на нем совершенно не сказывается состояние внешних электронных оболочек, которое определяется тем, входит ли атом в какое-нибудь соединение или остается свободным. Это чрезвычайно облегчает использование рентгеноскопического метода для аналитических целей, например, в геологии. Среди других применений рентгеновских лучей отметим возможность изучения структуры кристаллов и внутренних оболочек атомов, структурный анализ в химии и биологии (например, расшифровка структуры ДНК), диагностика и терапия в медицине, стерилизация пищевых продуктов, дефектоскопия в технике, криминалистика и т.д.
Поиск по сайту: |
 Рис. 31.3
Рис. 31.3
 .
.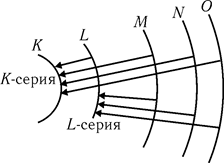 Рис. 31.4
Рис. 31.4
 ,
,
 .
.