 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение уравнения Шредингера для микрочастицы, находящейся в бесконечно глубокой потенциальной яме
Применим уравнение Шредингера к частице, находящейся в одномерной, бесконечно глубокой потенциальной яме шириной a (рис. 30.2). Внутри ямы (0<x<a) потенциальная энергия частицы равна нулю, а за пределами ямы (x<0 и a>x) — бесконечно велика. Очевидно, что частица может перемещаться только внутри ямы и не может выйти за ее пределы. Стационарное уравнение Шредингера для такого одномерного случая запишется так:
Обозначив
перепишем уравнение (16) в виде
Для решения линейного дифференциального уравнения второго порядка (30.18) составим характеристическое уравнение:
которое имеет два корня: k1=iq и k2= –iq. Тогда общее решение (18) будет иметь вид
где A и B — постоянные интегрирования. Для определения этих постоянных используем граничные условия, согласно которым вероятность нахождения частицы на краях ямы равна нулю: yy*=0 при x=0 или x=a. Отсюда A+B=0. Из первого условия следует A = –B. Тогда (19) преобразуется к виду
или с учетом формулы Эйлера (см. математическое введение)
Используя второе граничное условие, получаем
Таким образом, волновая функция микрочастицы может быть записана в виде
Значение второй постоянной интегрирования А нетрудно получить из условия нормировки волновой функции
откуда Для нахождения энергии микрочастиц определимиз (30.2) значение q и подставим его в выражение (17):
Как видно из (24), энергия микрочастицы в потенциальной яме может принимать только рад дискретных значений W1, W2…, которые называются уровнями энергии. При этом расстояние между соседними уровнями энергии возрастает по мере увеличения n:
Уровни энергии (24), а также распределение плотности вероятности Важная особенность в поведении микрочастицы внутри потенциальной ямы состоит в том, что ее энергия не может равняться нулю. Действительно, при n=0 и y=0 и тогда плотность вероятности нахождения микрочастицы в пределах потенциальной ямы yy*=0, что невозможно. Следовательно, предположение о том, что микрочастица может обладать нулевой энергией, неверно, так как приводит к парадоксальному выводу об ее исчезновении. В реальных условиях глубина потенциальной ямы конечна. Например, электрон внутри металла может двигаться свободно, однако его выходу в окружающее пространство препятствует потенциальный барьер, высота которого равна работе выхода электрона из металла. Решение уравнения Шредингера для этого случая приводит к следующим результатам: 1) энергия микрочастицы в такой яме также будет квантованной; 2) существует отличная от нуля вероятность того, что микрочастица с энергией, меньшей, чем высота потенциального барьера, ограничивающего яму, выйдет за ее пределы. По классическим представлениям такой процесс невозможен, поскольку он приводит к отрицательному значению кинетической энергии микрочастицы.
Поиск по сайту: |
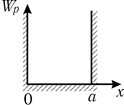 Рис. 30.2
Рис. 30.2
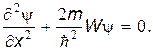
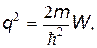
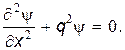
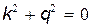 ,
,

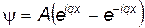

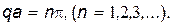
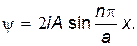
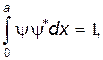
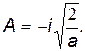
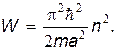
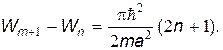
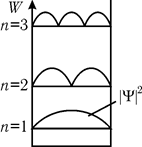 Рис. 3
Рис. 3
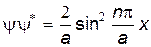 по координате x показаны на рис. 3. Видно, что для всех уровней энергии на стенках потенциальной ямы yy*=0. Кроме того, при данном n имеетсяn-1 промежуточная точка, где вероятность обнаружить микрочастицу равна нулю.
по координате x показаны на рис. 3. Видно, что для всех уровней энергии на стенках потенциальной ямы yy*=0. Кроме того, при данном n имеетсяn-1 промежуточная точка, где вероятность обнаружить микрочастицу равна нулю.