 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Типы межатомных связей и образование молекул
При сближении молекул между ними возникают силы межатомного взаимодействия, которые могут приводить к образованию молекул. Различают два вида межатомных (химических) связей — ионную и ковалентную. Природа ионной связи может быть объяснена в рамках классической физики как результат кулоновских сил притяжения между разноименно заряженными ионами. Типичными примерами молекул с ионной связью являются галоген-водороды — HCl, HBr и др. При сближении атомов водорода и галогена электроны атома водорода переходят во внешнюю, недостроенную оболочку атома галогена, достраивая ее до оболочки инертного газа. В результате этого возникает кулоновское притяжение между двумя разноименно заряженными ионами, обеспечивающее устойчивость образовавшейся полярной молекулы. Ковалентная связь имеет универсальный характер и образуется между любыми атомами. В наиболее чистом виде ковалентная связь проявляется в молекулах, состоящих из однотипных атомов, таких как H2, O2 и др. Природа ковалентной связи не может быть объяснена в рамках классической физики и требует использования квантово-механических представлений. Как показали теоретические расчеты и эксперименты, ковалентные связи обладают свойством насыщения, выражающимся в определенной валентности атомов и определенной направленности, формирующей пространственную структуру молекулы. При сближении атомов их электронные оболочки начинают перекрываться, что приводит к возникновению обменного взаимодействия, которое ответственно за образование ковалентной связи между атомами (см. прил. 7). Молекулярные спектры Полная внутренняя энергия W молекулы может быть представлена как сумма энергий электронов Wэл, колебательного движения ядер Wкол и вращательного движения Wвр молекулы как целого:
Электронная часть энергии молекулы, как и в атоме, может приобретать дискретный ряд значений: Перейдем теперь к рассмотрению энергии колебательного движения молекулы. Каждый атом молекулы имеет три степени свободы, поэтому если молекула состоит из N атомов, то общее число степеней свободы равно 3N. Из этого числа три степени свободы приходятся на поступательное и три степени - на вращательное движения молекулы как целого. Следовательно, число колебательных степеней свободы равно 3N–6 и молекула может совершить 3N–6 различных колебаний. С хорошим приближением можно считать, что эти колебания являются гармоническими с частотами n1, n2, ..., n3N-6. Энергия i-го гармонического колебания может быть выражена через частоту гармонического осциллятора формулой (см. § 30.6)
где ni=0, 1, 2, ... — колебательные квантовые числа. Таким образом, колебательная часть энергии молекулы квантуется, т.е. может иметь ряд дискретных значений. Вращательную энергию молекулы можно представить в виде
где J — момент инерции молекулы относительно оси, проходящей через ее центр масс; L = Jw — момент импульса. Как и для электрона в атоме (см. § 31.1), момент импульса молекулы квантуется:
где j — вращательное квантовое число, принимающее значения j=0, 1, 2, ... . Таким образом, вращательная энергия молекулы также квантуется, т.е. дискретна:
На основании изложенного можно заключить, что полная энергия молекулы
может принимать лишь дискретные значения. Теория и опыт показывают, что расстояние между электронными уровнями энергии значительно больше расстояний между колебательными уровнями, которые, в свою очередь, значительно больше расстояний между вращательными уровнями энергии:
Рис. 31.5 Энергетическая схема уровней двухатомной молекулы показана на рис. 31.5, где В общем случае при поглощении фотона энергии hn молекула может перейти в состояние с возбуждением вращательных, колебательных и электронных уровней энергии:
где, например, В миллиметровом диапазоне радиоволн энергия фотона настолько мала, что ее достаточно лишь для возбуждения вращательных уровней (DWвр ≠ 0, DWкол=0, DWэл=0). Возникает вращательный спектр, состоящий из ряда близко расположенных линий. Частоты линий этого спектра находятся из условия
Для вращательных уровней действует правило отбора: возможны переходы только между соседними уровнями, поэтому j'=j+1. Тогда
Измерив на опыте частоту вращательной линии спектра, можно с помощью (31.12) найти момент инерции и затем — равновесное состояние между ядрами в двухатомной молекуле или размеры более сложных молекул.
При увеличении частоты квантов становятся возможными переходы с возбуждением колебательных состояний. При этом также могут возбуждаться вращательные уровни энергии. Возникает колебательно-вращательный спектр (рис. 31.6), расположенный в инфракрасной области спектра (от 800 до 5000 нм). Этот вид спектра является полосатым: каждой полосе соответствует определенная колебательная частота, а тонкая структура полос обусловлена переходами молекулы на вращательные уровни энергии (рис. 31.6). Измерив на опыте частоты колебательных линий спектра, можно рассчитать упругие константы молекулы и определить энергию ее диссоциации. И, наконец, в видимой и ультрафиолетовой части электромагнитного диапазона располагается электронно-колебательный спектр (DWвр ≠ 0, DWкол ≠ 0, DWэл = 0). Для его регистрации применяют приборы, где вращательная структура спектра не разрешается: в пределах одной колебательной линии происходит слияние всех вращательных линий. Колебательная структура электронно-колебательных спектров проявляется лишь для самых простых молекул. Сложные многоатомные дают, как правило, сплошные спектры поглощения и излучения. Спектры поглощения молекул в большинстве случаев строго индивидуальны: каждая молекула имеет свой спектр. По виду спектра можно проводить идентификацию молекул, а по его интенсивности можно определять концентрацию соответствующего вещества. Тем самым представляется возможность проводить спектральный анализ сложных химических смесей.
Поиск по сайту: |
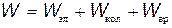 .
. ,
,  , ... . Состояние с наименьшим значением энергии
, ... . Состояние с наименьшим значением энергии  ,
,
 ,
,
 ,
,
 .
.

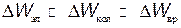 .
.
 ,
,  ,
,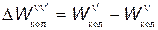 — разность энергий между колебательными уровнями n и n'.
— разность энергий между колебательными уровнями n и n'. .
. .
.
 Рис. 31.6
Рис. 31.6