 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Квантово-механическая модель атома водорода
Потенциальная энергия атома водорода определяется выражением (29.30), поэтому уравнение Шредингера применительно к атому водорода имеет вид
Волновая функция y в данном случае — это функция трех пространственных координат x, y, z. Решение уравнения (31.1) — довольно сложная математическая задача, поэтому наметим лишь схему решения. Прежде всего осуществляют переход от декартовой системы координат (x, y, z) к сферической (r, q, j) — см. рис. 1.4. В сферических координатах уравнение Шредингера (31.1) разбивается на три уравнения, каждое из которых содержит лишь одну переменную r, q или j. Это в значительной степени упрощает решение задачи, поскольку каждоеиз полученных уравнений — это обыкновенное дифференциальное уравнение. Решение уравнения относительно r позволяет найти значения энергии атома водорода. Оказывается, что энергия атома квантуется, т.о. принимает дискретный ряд значений
Здесьn=1, 2, … называется главным квантовым числом. Выражение (31.2) совпадает с результатом, полученным в теории Бора (29.32), однако при его выводе не вводились никакие дополнительные предположения (постулаты),как в теории Бора. Решив уравнение относительно q, можно найти момент импульса электрона. Оказывается, что допустимые значения момента импульса принимают дискретный ряд значений, определяемых орбитальным квантовым числом l:
Орбитальное квантовое число l принимает целочисленные значения в интервале от 0 до n–1. Выражение (31.3) формально совпадает с правилом квантования орбит Н. Бора (29.24), однако есть два принципиальных отличия. Во-первых, в теории Н. Бора l может принимать любые, сколь угодно большие значения. В квантово-механической модели атома максимальное значение орбитального квантового числа l ограничено главным квантовым числом: при данном n орбитальное квантовое число имеет верхний предел n–1. Во-вторых, в квантово-механической модели имеется состояние, характеризуемой значением орбитального квантового числа l=0. В теории Бора такое значение l недопустимо, поскольку при этом скорость электрона равна нулю, что противоречит ядерной модели атома Бора-Резерфорда. Это противоречие подчеркивает недопустимость описания движения электрона как движения по строго определенной орбите. И наконец, решая уравнение Шредингера относительно координаты j можно найти проекций момента импульса на выделенное направление, например, направление внешнего магнитного поля
где m — магнитное квантовое число, которое принимает целочисленные значения в интервале, ограниченном орбитальным квантовым числом l: m=–l, -(l-1),…,-1, 0, +1,…, l-1, l. Дискретный характер проекции момента импульса Lz на вселенное направление получил название пространственного квантования: во внешнем магнитном поле момент импульса электрона может принимать лишь такие направления, проекция которых на направление этого поля выражается целым числом (в единицах ħ). На рис. 31.1 показаны возможные ориентации вектора
Таким образом, состояние электрона в атоме описывается тремя квантовыми числами n, l, т, значения которых определяют величину энергии, момента импульса и проекции момента импульса на выделенное направление. Энергия атома водорода зависит только от главного квантового числа. Некоторому значению этого числа соответствуют n возможных значений числа l и 2l+1 значений магнитного квантового числа. Главному квантовому числу п=1 соответствуют l=0 и т=0. Получаем одно состояние с волновой функцией y100. Главному квантовому числу n=2 соответствуют числа l=0,1 и т=–1, 0, +1. В результате при n=2 получаются четыре состояния y200, y21,-1, y210, y211. В общем случае произвольного n получается n2 различных состояний. Все эти состояния характеризуются одним и тем же значением энергии. Состояния с одинаковым значением энергии, но различными квантовыми числами l и т называются вырожденными. При наложении внешнего магнитного пиля вырождение снимается: уровни энергии расщепляются на ряд близко расположенных подуровней, что спектрально проявляется в расщеплении соответствующих спектральных линий (эффект Зеемана). Аналогичный эффект называется также внешним электрическим полем (эффект Штарка).
Поиск по сайту: |


 ,
,
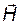 :
: ,
,
 при некоторых значениях орбитального квантового числа l.
при некоторых значениях орбитального квантового числа l. Рис. 31.1
Рис. 31.1