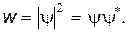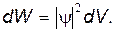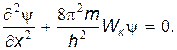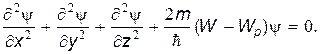Волновая функция и ее статистический смысл

В классической механике можно дать однозначный ответ на вопрос, находится ли частица в данный момент времени в определенной области пространства. Так, если выделить некоторый объем пространства, содержащий участок траектории частицы, то, зная уравнение ее движения, можно с достоверностью установить, будет ли она в данный момент времени находиться в этом объеме или нет. Если же траектория частицы не проходит через выделенный объем пространства, то можно утверждать, что частицы там не может быть ни в какой момент времени.

Таким образом, классическому описанию движения частицы соответствует формальная логика с двумя элементарными понятиями «да» и «нет». Закономерности классической механики и формальной логики неприменимы для описания движения микрочастиц, поскольку последние характеризуются волновыми свойствами. При этом следует участь также, что квантово–механические закономерности, правильно описывая явления микромира, не имеют той же степени наглядности, что и классические закономерности.

Для описания волновых свойств микрообъектов в квантовой механике вводится величина y, которая называется волновой (или «пси») функцией. Движению микрочастиц сопоставляется уравнение некоторой волны, которое в простейшем случае имеет вид

(8)

Формально уравнение (8) совпадает с классическим уравнением механической или электромагнитной волны. Однако физический смысл волновой функции принципиально отличается от классического. В механической волке волновой функции y соответствует определенная деформация упругой среды (для данной точки пространства в данный момент времени), а в электромагнитной волне — соответствующие значения напряженно стой электрического и магнитного полей.

В квантовой механике волновой функции y придается следующий физический смысл: квадрат модуля волновой функции определяет вероятность нахождения микрочастицы в данной точке пространства (точнее, в единичном объеме вблизи от заданной точки пространства):

(9)

Вероятность обнаружения частицы в некотором объеме dV определяется очевидным соотношением

(10)

Из смысла волновой функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.

Волновая функция (вместе со своими производными) должна быть конечной, однозначной и непрерывной. Кроме того, волновая функция должна удовлетворять условию нормировки:

(11)

Интеграл (11) определяет вероятность того, что микрочастица находится в какой-либо точке пространства, т.е. вероятность достоверного события, которая равна единице.

Лекція 41.

Рiвняння Шредiнгера. Частинка в нескiнченно глибокiй потенцiальнїй ямi. Квантовий гармонiчний осцилятор. Тунельний ефект.

Уравнение Шредингера

Для того чтобы найти волновую функцию y, характеризующую состояние микрочастицы или системы микрочастиц, необходимо решить волновое уравнение, которое было получено Э. Шредингером в 1926 г. Уравнение Шредингера — основа квантовой (волновой) механики, так же как уравнения Ньютона — основные уравнения классической механики. Как и уравнения Ньютона, уравнение Шредингера не может быть выведено из других более элементарных принципов и вводится в квантовую механику как постулат. Справедливость уравнения Шредингера определяется тем, что все выводы, полученные из его решений и доступные опытной проверке, подтверждались. Тем не менее, дадим некоторое методическое обоснование этого уравнения.

Продифференцируем дважды по координате x волновую функцию (8):

или

(12)

Подставим вместо длины волныl ее значение по формуле де Бройля:

Учитывая, что

где W_к — кинетическая энергия частицы, получаем

Заменив в этом уравнении кинетическую энергию частицы на разность между полной и потенциальной энергией: W_к =W–W_р. Тогда

(13)

Последнее уравнение и представляет собой одномерное стационарное уравнение Шредингера. Если ввести постоянную ħħ=h/2p, то уравнение (13) можно переписать в виде

(14)

В общем (трехмерном) случае уравнение Шредингера имеет вид

(15)

В тех случаях, когда потенциальная энергия системы изменяется со временем, необходимо использовать более сложное временное уравнение Шредингера:

Поиск по сайту: