 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Описание установки и метода измерений. Маятник Максвелла представляет собой массивный диск (маховик)
Как известно, закон сохранения механической энергии для тела массы m, одновременно вращающегося с угловой скоростью w и движущегося поступательно со скоростью J, вид: где П=mgh – потенциальная энергия тела массы m, поднятого на высоту h в поле силы тяжести; Обозначая натяжение каждой нити через Т/2, можно записать уравнения основного закона динамики для этих двух движений:
где m – масса маятника, g – ускорение свободного падения, b – угловое ускорение маятника, d – диаметр вала. Выражение Из кинематики вращательного движения известно, что угловое ускорение b связано с линейным ускорениемaсоотношением a=br (для нашего случая Исключая из системы (2) T, учитывая связь между величинами a и b, а также уравнение (3), получим формулу для определения момента маятника
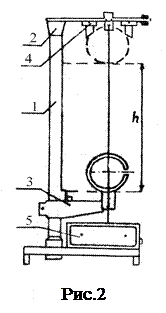
Таким образом, для нахождения момента инерции маятника нужно измерить время его падения t с определенной высоты h. Схема экспериментальной установки изображена на рис. 2. Подвес маятника смонтирован на вертикальной стойке 1, на которой закреплены два кронштейна – верхний 2 и нижний 3 с фотоэлектрическими датчиками. В верхнем положении маятник удерживается электромагнитом 4. Указатель на нижнем кронштейне позволяет измерить высоту, с которой падает маятник, по миллиметровой шкале на стойке прибора. Время падения маятника измеряется электронным секундомером, находящимся в блоке управления 5. Измерения моментов инерции проводятся с тремя кольцами, надеваемыми на диск маятника. Выполнение работы 1. Надеть на диск одно из колец. В нижнем положении маятник с кольцом должен быть примерно на 2 мм ниже оси фотоэлектрического 2..После включения установки в сеть нажать на клавишу “СЕТЬ”, при этом на табло электронного секундомера должны высвечиваться нули. При отжатой клавише “ПУСК” намотать равномерно на вал маятника нить, виток к витку. В верхнем положении маятник должен удерживаться электромагнитом. 3. Нажав на клавишу “ПУСК”, маятник начнет двигаться вниз. После окончания падения секундомер выключается автоматически. Показания секундомера следует занести в табл. 1. 4. Для проведения измерений с другим кольцом нужно отжать клавишу “ПУСК” и нажать на клавишу “СБРОС”, при этом секундомер обнуляется. С каждым кольцом необходимо провести не менее пяти измерений и найти среднее значение времени падения маятника. 5. По формуле (4) рассчитать момент инерции J системы с каждым кольцом. В нашем случае масса маятника равна сумме масс вала, диска и кольца, т.е. m=mв+mд+mк. Их величины указаны на них с точностью 6. Измеренные значения моментов инерции маятника сравнить с теоретическими, рассчитанными исходя из того, что элементы маятника – вал, диск и кольца считаются телами простой геометрической формы (см. рис. 5, стр. 6). Внутренний и внешний диаметры колец соответственно равны (86 7. Для одного из измеренных моментов инерции необходимо оценить абсолютную и относительную погрешность измерений.
Контрольные вопросы 1. Что называется моментом инерции тела, относительно неподвижной оси вращения? 2. Может ли твердое тело иметь несколько моментов инерции? 3. Сформулируйте основной закон динамики вращательного движения. 4. Объясните, как при движении маятника Максвелла проявляется действие основных законов динамики поступательного и вращательного движений. 5. Почему маятник, достигнув нижнего положения, начинает подниматься вверх? РАБОТА № 5-3
Поиск по сайту: |
 Маятник Максвелла представляет собой массивный диск (маховик), насаженный на вал (рис. 1.). Диск подвешен на двух тонких нерастяжимых нитях, наматываемых на вал, а на этот диск надеваются толстостенные металлические кольца. При раскручивании нитей маятник опускается под действием силы тяжести с постоянным ускорением a, совершая одновременно вращательное и поступательное движения.
Маятник Максвелла представляет собой массивный диск (маховик), насаженный на вал (рис. 1.). Диск подвешен на двух тонких нерастяжимых нитях, наматываемых на вал, а на этот диск надеваются толстостенные металлические кольца. При раскручивании нитей маятник опускается под действием силы тяжести с постоянным ускорением a, совершая одновременно вращательное и поступательное движения.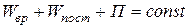 , (1)
, (1)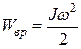 – кинетическая энергия вращающегося тела, где J – момент инерции этого тела;
– кинетическая энергия вращающегося тела, где J – момент инерции этого тела; 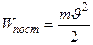 – кинетическая энергия тела, движущегося поступательно.
– кинетическая энергия тела, движущегося поступательно.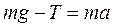 и
и 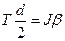 , (2)
, (2) представляет собой момент силы относительно вала.
представляет собой момент силы относительно вала. - радиус вала). Очевидно, что при раскручивании нитей маятник будет опускаться с некоторой высоты h по закону кинематики равноускоренного движения
- радиус вала). Очевидно, что при раскручивании нитей маятник будет опускаться с некоторой высоты h по закону кинематики равноускоренного движения  (3)
(3) ,где t – время падения маятника с высоты h. Поскольку
,где t – время падения маятника с высоты h. Поскольку 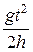 >>1, то
>>1, то 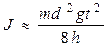 (4)
(4) датчика(перекрывать его). Высота падения h указывается преподавателем.
датчика(перекрывать его). Высота падения h указывается преподавателем. 0,01 г.(Точность измерения всех масс
0,01 г.(Точность измерения всех масс  t,
c
t,
c