 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот процесс совершается через равные промежутки времени, то колебание называется периодическим. Несмотря на большое разнообразие колебательных процессов как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими, которые совершаются по закону синуса (или косинуса). Предположим, что они описываются законом
Здесь x - смещение (отклонение) колеблющейся системы от положения равновесия; А - амплитуда, т.е. максимальное смещение от положения равновесия, φо - начальная фаза колебания (при t=0); t - время колебаний; ω - круговая частота (или угловая скорость) колебаний. ω связана с частотой колебания Т - период - время одного полного колебания.
Систему, закон движения которой имеет вид (1), называют одномерным классическим гармоническим осциллятором. Хорошо известным примером гармонического осциллятора является тело (шарик), подвешенное на упругой пружине. По закону Гука при растяжении или сжатии пружины возникает противодействующая сила, пропорциональная растяжению или сжатию х, т.е. тело будет совершать гармонические колебания под действием силы упругости пружины F=-kx. Однако гармонические колебания возникают под действием не только упругих, но и других сил, по природе не упругих, но для которых остается справедливым закон F=-kx. Такие силы получили название квазиупругих. Как известно, движение системы под действием силы описывается II-м законом Ньютона: ma =F, где a - ускорение колеблющейся системы Для гармонических колебаний F=-kx. Тогда второй закон Ньютона будет иметь вид неполного дифференциального уравнения второго порядка
или уравнение движения классического осциллятора, где Решением данного уравнения (3) является выражение (1), что нетрудно проверить, дифференцируя дважды (1) по времени и подставляя в уравнение (3). При этом получим, что Для упрощения записи в дальнейшем можно положить начальную фазу нулю (φо=0), тогда уравнение (1) будет иметь вид
Видно, что скорость при гармонических колебаниях тоже изменяется по гармоническому закону, но опережает смещение по фазе на Ускорение тела при гармонических колебаниях равно:
Сравнение этого выражения (6) с (1) показывает, что ускорение и смещение находятся в противофазе (рис.2). Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Кинетическая энергия осциллятора при гармоническом колебании с учетом (4) и (5) имеет вид: Потенциальная энергия:
Полная энергия гармонического осциллятора в процессе колебаний не меняется. Действительно:
Из последнего выражения видно, что полная механическая энергия осциллятора пропорциональна квадрату амплитуды и не зависит от времени. Кинетическая и потенциальная энергии изменяются по гармоническому закону, как Рассмотрим некоторые из классических гармонических осцилляторов.
Поиск по сайту: |
 (1)
(1) - фаза колебаний. Физический смысл фазы в том, что она определяет смещение х в данный момент времени,
- фаза колебаний. Физический смысл фазы в том, что она определяет смещение х в данный момент времени, и периодом колебания Т:
и периодом колебания Т:  , (2)
, (2) Если в уравнении (1) положить начальную фазу φо=0, то график зависимости смещения х от времени или график гармонического колебания будет иметь вид, представленный на рис.1.
Если в уравнении (1) положить начальную фазу φо=0, то график зависимости смещения х от времени или график гармонического колебания будет иметь вид, представленный на рис.1. , (3)
, (3) .
.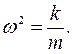 (4)
(4) (1΄)
(1΄)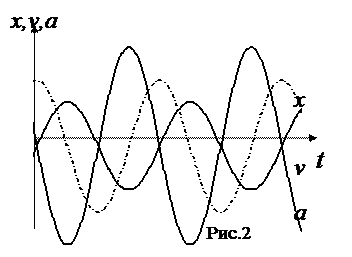 Скорость гармонически колеблющегося тела можно найти, дифференцируя по времени уравнение (1΄):
Скорость гармонически колеблющегося тела можно найти, дифференцируя по времени уравнение (1΄): или
или  . (5)
. (5) (по времени на Т/4).
(по времени на Т/4). , или
, или (6)
(6)
 , а так как "k" связано с собственной частотой колебания осциллятора (
, а так как "k" связано с собственной частотой колебания осциллятора ( 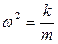 ), то
), то

 и
и 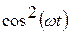 , но когда одна из них увеличивается, другая уменьшается. Это означает, что процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно.
, но когда одна из них увеличивается, другая уменьшается. Это означает, что процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно.