 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ИЗ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Принадлежности: прибор для определения модуля сдвига из крутильных колебаний, секундомер, микрометр, масштабная линейка. Краткая теория Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Этот вид деформации возникает под действием сил, приложенных к двум диагонально противоположным граням тела, касательным к той поверхности, на которую они действуют (рис.1).
Измеряется тангенциальное напряжение в тех же единицах, что и давление. Деформация сдвига характеризуется величиной относительного сдвига g. Чтобы объяснить, что такое относительный сдвиг, обратимся к рис.1. Выберем какие-нибудь точки тела, лежащие на одной прямой, например, точки А и В. При деформации сдвига величины смещения выбранных точек АА¢ и ВВ¢ называются абсолютным сдвигом. Абсолютный сдвиг для различных точек различен (АА¢ ¹ ВВ¢ ), но отношение каждого этого сдвига к расстоянию до точки О будет одно и то же: Если деформации малы, то По закону Гука для малых деформаций относительный сдвиг пропорционален тангенциальному напряжению, т.е. Величина G называется модулем сдвига. Таким образом, модуль сдвига численно равен тангенциальному напряжению, которое возникло бы в твердом теле при относительном сдвиге, равном единице. В.СИ модуль сдвига измеряется в Н/м2 (Па), а в системе СГС - в дин/см2.
Деформация кручения возникает в образце (стержне, проволоке и т.п.), если одно сечение образца закреплено неподвижно, а во втором действуют две равные по модулю и противоположные по направлению касательные силы (пара сил), момент Под действием крутящего момента чем дальше эти сечения расположены от сечения, закрепленного неподвижно. Угол поворота j верхнего сечения называют углом кручения. В результате деформации кручения возникает перекос на угол j образующих цилиндрической поверхности стержня. По закону Гука угол кручения j связан с моментом
где N - модуль кручения, который показывает, какой момент нужно приложить, чтобы закрутить стержень на угол в один радиан. Найдем теперь связь между модулем сдвига и модулем кручения. Для этого предположим, что стержень с радиусом r и длиной L из материала, модуль сдвига которого G, закручен под действием момента Все кубики, вырезанные из такого кольца (рис.3,в), будут иметь одинаковую деформацию сдвига на один и тот же угол g. Таким образом, деформация кручения свелась к деформации сдвига. Из рис.3а видно, что
или Определим теперь упругую касательную силу, действующую на поверхность кольца, площадь которого
С другой стороны, элементарный момент dM равен Тогда для всего стержня полный момент М равен
После интегрирования получим: где Д=2r - диаметр стержня. Подставляя (5) в (3), получим соотношение между модулем кручения N и модулем сдвига G:
Поиск по сайту: |
 Касательная сила Ft, действующая на единицу поверхности, называется тангенциальным (касательным) напряжением:
Касательная сила Ft, действующая на единицу поверхности, называется тангенциальным (касательным) напряжением:  (1)
(1)
 Поэтому можно сказать, что относительный сдвиг есть измеренный в радианах угол сдвига.
Поэтому можно сказать, что относительный сдвиг есть измеренный в радианах угол сдвига. (2)
(2) В данной лабораторной работе модуль сдвига определяется косвенно - из деформации кручения. Рассмотрим более подробно этот вид деформации и ее связь с деформацией сдвига.
В данной лабораторной работе модуль сдвига определяется косвенно - из деформации кручения. Рассмотрим более подробно этот вид деформации и ее связь с деформацией сдвига. которых относительно центра этого сечения направлен по оси образца (рис.2).
которых относительно центра этого сечения направлен по оси образца (рис.2). (3)
(3)

 (4)
(4) . Согласно (1) и (2),
. Согласно (1) и (2),

 .
. .Очевидно, что для однородного стержня
.Очевидно, что для однородного стержня  . Тогда
. Тогда  , (5)
, (5)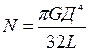 . (6)
. (6)