 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
ПО МЕТОДУ СТОКСА Принадлежности:стеклянный сосуд, наполненный вязкой жидкостью, шарики из свинца, секундомер, измерительный микроскоп, масштабная линейка. Краткая теория Реальная жидкость, в отличие от идеальной, обладает вязкостью (внутренним трением), обусловленной сцеплением (взаимодействием) между ее молекулами. При движении жидкости между ее слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения, вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения (или импульса), что приводит к его торможению.
Рассмотрим жидкость, движущуюся в направлении оси Х (рис.1) Пусть слои жидкости движутся с разными скоростями. На оси Z возьмем две точки, находящиеся на расстоянии dz. Скорости потока отличаются в этих точках на величину dx. Отношение Сила внутреннего трения (вязкости) по Ньютону, действующая между двумя слоями жидкости, пропорциональна площади соприкасающихся слоев ΔS и градиенту скорости: Знак минус означает, что импульс движения переносится в направлении уменьшения скорости, η- коэффициент внутреннего трения, или коэффициент вязкости. Иногда коэффициент вязкости η, определяемый формулой (1), называют коэффициентом динамической вязкости в отличие от кэффициента кинематической вязкости, равного отношению η/ρ, где ρ - плотность жидкости.
Как следует из формулы (1), в системе СИ коэффициент вязкости η измеряется в Н·с/м2=Па·с (паскаль-секунда), а в системе СГС в дн·с/см2=г/см·с (Пуаз). Рассмотрим падение твердого тела в форме шарика в вязкой жидкости (рис.2). На шарик действуют три силы: сила тяжести f1 = mg, подъемная, или выталкивающая сила (закон Архимеда), – f2 и сила сопротивления движению шарика, обусловленная силами внутреннего трения жидкости, - f3. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движении, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика. Таким образом, при вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость. Сила сопротивления движению шарика определяется формулой Стокса где v – скорость движения шарика, r – его радиус. С учетом действия на шарик трех сил уравнение движения в общем виде запишется следующим образом: или в скалярной записи с учетом знака сил
где ρ – плотность шарика, ρ1 – плотность вязкой жидкости, g – ускорение свободного падения. Все три силы, входящие в правую часть уравнения (3), будут направлены по вертикали: сила тяжести – вниз, подъемная сила и сила сопротивления – вверх. Сила сопротивления с увеличением скорости движения шарика возрастает. При некоторой скорости шарика сила сопротивления становится равной сумме сил тяжести, т.е. f3 = f2 +f1. Таким образом, равнодействующая этих сил обращается в нуль. Это означает, что уравнение (3) принимает вид Так как m≠0, то Таким образом, по достижении шариком скорости v0 далее он движется с постоянной скоростью и уравнение (3) принимает следующий вид: Решая уравнение (4) относительно коэффициента внутреннего трения, получаем где d – диаметр шарика. Зная скорость установившегося движения шарика Выполнение работы Задание 1. Определение диаметров шариков. Измерение диаметров шариков производится с помощью микроскопа.
Количество шариков, необходимое для выполнения работы, указывается преподавателем. Задание 2. Определение коэффициента вязкости исследуемой жидкости. Прибор для определения коэффициента вязкости жидкости состоит из стеклянного цилиндра, наполненного исследуемой жидкостью и имеющего горизонтальные, подвижные металлические обручи 1 и 2 (рис.4). Расстояние между обручами
Расстояние В нашем случае ρ = 11,30 г/см3, ρ1 = 0,96 г/см3. Так как внутреннее трение жидкостей сильно зависит от температуры, то необходимо отметить температуру во время проведения опыта. Проведя эксперимент с указанным числом шариков, вычисляют значения коэффициентов вязкости η для каждого шарика, а затем вычисляют среднюю абсолютную и относительную ошибки измерений. Полученные результаты заносятся в таблицу
Контрольные вопросы 1. 1.Объясните механизм внутреннего трения в жидкостях 2. Объясните физический смысл коэффициента вязкости. 3. В каких единицах измеряется коэффициент вязкости в ед.СИ и системе СГС? 4. Выведите рабочую формулу (6), поясните этот вывод. 5. Как зависит коэффициент вязкости от температуры? 6. Что представляет собой градиент скорости? Дайте определение этой величины.
РАБОТА № 12
Поиск по сайту: |
 Таким образом, при переносе импульса от слоя к слою происходит изменение импульса этих слоев (увеличение или уменьшение). Это значит, что на каждый из этих слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона). Эта сила называется силой трения между слоями жидкости, движущимися с различными скоростями (внутреннее трение).
Таким образом, при переносе импульса от слоя к слою происходит изменение импульса этих слоев (увеличение или уменьшение). Это значит, что на каждый из этих слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона). Эта сила называется силой трения между слоями жидкости, движущимися с различными скоростями (внутреннее трение). называется градиентом скорости – векторная величина, численно равная изменению скорости на единицу длины в направлении, перпендикулярном скорости, и направленная в сторону возрастания скорости.
называется градиентом скорости – векторная величина, численно равная изменению скорости на единицу длины в направлении, перпендикулярном скорости, и направленная в сторону возрастания скорости. –
–  ΔS. (1)
ΔS. (1) Физический смысл коэффициента вязкости η заключается в том, что он численно равен силе внутреннего трения, возникающей на единице площади соприкасающихся слоев жидкости при градиенте скорости между ними, равном единице.
Физический смысл коэффициента вязкости η заключается в том, что он численно равен силе внутреннего трения, возникающей на единице площади соприкасающихся слоев жидкости при градиенте скорости между ними, равном единице. , (2)
, (2)
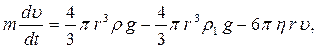 (3)
(3)
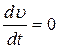 и
и 
 (4)
(4) (5)
(5) , где
, где  - длина пути, проходимого шариком при установившемся движении, t – время его движения, а также плотности ρ и ρ1 и размеры шарика, можно вычислить значение коэффициента вязкости для данной жидкости по формуле.
- длина пути, проходимого шариком при установившемся движении, t – время его движения, а также плотности ρ и ρ1 и размеры шарика, можно вычислить значение коэффициента вязкости для данной жидкости по формуле.  (6)
(6) Для измерения диаметра шарика необходимо поступить следующим образом. Положив шарик внутрь шайбы на предметном столике микроскопа, включить осветитель. Регулировкой положения осветителя и зеркальца осветить шарик снизу. При правильной регулировке осветителя и зеркальца наблюдаемое в окуляр поле зрения должно быть наиболее ярким. Вращая окуляр, добиться резкого изображения перекрестия нитей. Установить тубус на такую высоту, чтобы отчетливо были видны края шарика (при правильной регулировке осветителя и зеркальца в поле зрения должно быть видно изображение шарика в виде черного круглого пятна на фоне яркого поля зрения). Перемещая при помощи микрометрического винта тубус микроскопа, навести вертикальную нить окуляра последовательно на края шарика, чтобы нить казалась касательной шарику (рис.3). В положениях 1 и 2 снимаются отсчеты а1 и а2 по шкале в миллиметрах, а по барабану - отсчеты, выраженные в сотых долях миллиметра (один полный оборот барабана равен горизонтальному перемещению тубуса на один миллиметр). Разность между двумя отсчетами ( а1 и а2) дает диаметр шарика d. Шарики имеют не совсем правильную форму, поэтому необходимо диаметр каждого шарика измерять не менее трех раз, поворачивая после каждого измерения шарик на предметном столике микроскопа с помощью пинцета. Шарики с ярко выраженными поверхностными дефектами использовать для опыта не рекомендуется.
Для измерения диаметра шарика необходимо поступить следующим образом. Положив шарик внутрь шайбы на предметном столике микроскопа, включить осветитель. Регулировкой положения осветителя и зеркальца осветить шарик снизу. При правильной регулировке осветителя и зеркальца наблюдаемое в окуляр поле зрения должно быть наиболее ярким. Вращая окуляр, добиться резкого изображения перекрестия нитей. Установить тубус на такую высоту, чтобы отчетливо были видны края шарика (при правильной регулировке осветителя и зеркальца в поле зрения должно быть видно изображение шарика в виде черного круглого пятна на фоне яркого поля зрения). Перемещая при помощи микрометрического винта тубус микроскопа, навести вертикальную нить окуляра последовательно на края шарика, чтобы нить казалась касательной шарику (рис.3). В положениях 1 и 2 снимаются отсчеты а1 и а2 по шкале в миллиметрах, а по барабану - отсчеты, выраженные в сотых долях миллиметра (один полный оборот барабана равен горизонтальному перемещению тубуса на один миллиметр). Разность между двумя отсчетами ( а1 и а2) дает диаметр шарика d. Шарики имеют не совсем правильную форму, поэтому необходимо диаметр каждого шарика измерять не менее трех раз, поворачивая после каждого измерения шарик на предметном столике микроскопа с помощью пинцета. Шарики с ярко выраженными поверхностными дефектами использовать для опыта не рекомендуется. задается преподавателем.
задается преподавателем. Для измерения коэффициента внутреннего трения в данной работе используются маленькие шарики из свинца. Измерив предварительно диаметры шариков, опускают их в цилиндр с вязкой жидкостью (касторовое масло) через отверстие А в крышке цилиндра. Скорости шариков довольно значительны, поэтому глаз наблюдателя необходимо установить против верхнего обруча 1 так, чтобы обруч сливался в одну полосу. Считая движение установившимся к моменту прохождения шариком верхнего обруча, в момент прохождения шарика через верхний край обруча 1 пускают секундомер. После этого точно таким же образом наблюдают прохождение шариком нижнего обруча 2 и останавливают секундомер в момент прохождения шариком верхнего края обруча 2. Так определяется время t движения шарика между обручами 1 и 2.
Для измерения коэффициента внутреннего трения в данной работе используются маленькие шарики из свинца. Измерив предварительно диаметры шариков, опускают их в цилиндр с вязкой жидкостью (касторовое масло) через отверстие А в крышке цилиндра. Скорости шариков довольно значительны, поэтому глаз наблюдателя необходимо установить против верхнего обруча 1 так, чтобы обруч сливался в одну полосу. Считая движение установившимся к моменту прохождения шариком верхнего обруча, в момент прохождения шарика через верхний край обруча 1 пускают секундомер. После этого точно таким же образом наблюдают прохождение шариком нижнего обруча 2 и останавливают секундомер в момент прохождения шариком верхнего края обруча 2. Так определяется время t движения шарика между обручами 1 и 2. между обручами измеряется масштабной линейкой. Подставляя в формулу (6) значения
между обручами измеряется масштабной линейкой. Подставляя в формулу (6) значения 