 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ИССЛЕДОВАНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Приборы и принадлежности: маятник Обербека с электронным блоком управления, набор грузов. Описание установки и метода измерений. Маятник Обербека (рис.1) представляет собой крестовину, состоящую из четырех взаимно перпендикулярных одинаковых стержней 1, которые ввинчены в металлическую втулку 2 радиусом r. Эта крестовина свободно вращается вокруг горизонтальной оси. На стержни надеты одинаковые грузы 3 массой m' ,которые могут быть закреплены на различных расстояниях l от оси вращения. На ось вращения маятника посажены два легких шкива 4 с различными радиусами R1 и R2. На один из шкивов наматывается шнур к свободному концу которого, перекинутого через блок, прикрепляется платформа 5. Если на платформу поместить груз массой m, то они, падая вниз и натягивая нить, будут приводить крестовину в равноускоренное вращательное движение. Перемещая грузы m' по стержням, можно менять момент инерции маятника. Беря разные грузы m, а также шкивы разного радиуса, можно менять момент вращающей силы: M = F×R , (1)
Имеющаяся на стойке установки миллиметровая шкала позволяет измерить путь h, проходимый платформой с грузом m при их падении. На верхнем 6 и нижнем 7 кронштейнах расположены фотоэлектрические датчики. При пересечении светового луча движущимся грузом сигнал первого датчика включает электронный секундомер, а сигнал второго датчика выключает его. На индикаторе секундомера 8 высвечивается время t прохождения грузом пути h (расстояния между кронштейнами). Ускорение a груза может быть найдено на основе закона кинематики равноускоренного движения: Зная ускорение груза, можно по второму закону Ньютона определить силу Fн натяжения нити: ma = mg - Fн, где g- ускорение свободного падения. Тогда Fн = m (g-a) (3) Такая же сила со стороны нити приложена по касательной к шкиву крестовины. Момент этой силы М относительно оси вращения, согласно (1), будет равен: Этот момент силы в соответствии с основным законом динамики вращательного движения M = I×b (5) вызывает ускоренное вращение крестовины с угловым ускорением b, (I - момент инерции крестовины относительно оси вращения). Величина b может быть определена из взаимосвязи линейного и углового ускорения: На основании экспериментальных данных могут быть найдены: момент силы M, действующей на крестовину, и угловое ускорение b крестовины. Это позволяет проверить справедливость основного закона динамики вращательного движения (5), линейную зависимость b от M, а также определить момент инерции I системы. При этом считается, что силой трения в подшипнике маятника и силами сопротивления, действующими на движущиеся тела, можно пренебречь.
где r = (20±0,1) мм - радиус втулки, а = (10±0,1) мм - цена одного деления шкалы стержня, l0 = (20±0,1) мм - размер цилиндрического груза m¢ по его высоте.
Основные данные установки: радиусы шкивов R1 = (21±0,1) мм и R2 = (44±0,1) мм; масса одного груза m¢ = (189±0,01) г; массы грузов, помещаемых на платформу, m = (41±0,01) г; масса платформы равна (53±0,01) г. Выполнение работы. В данной работе проверяется основной закон динамики вращательного движения (5) и выполняются два задания. Задание 1. Определение момента инерции маятника I для различных значений момента силы M. Для этого случая I=M1 /b1= M2 /b2 …= Mi /bi (7) 1. Закрепить все четыре груза m¢ на одинаковом расстоянии l1, (примерно 60-70 мм) от оси вращения маятника, закрепить шнур на одном из шкивов с радиусом R1 или R2, между кронштейнами 6 и 7 установить определенное расстояние h. 2. После включения установки в сеть нажать клавишу "СЕТЬ" при этом на табло электронного секундомера должны высвечиваться нули. При утопленной клавише "ПУСК" после нажатия клавиши "СБРОС" шнур наматывается на шкив так, чтобы нижний край платформы совпал с чертой на верхнем кронштейне. После отжатия клавиши "ПУСК" платформа будет удерживаться электромагнитным тормозом. 3. На платформу положить груз m1. После нажатия клавиши "ПУСК" ток в цепи электромагнита выключается, платформа с грузом освобождается и приходит в движение. Одновременно начинается отсчет времени. Время t прохождения платформы с грузом расстояния h считывается с индикатора секундомера. Измерения повторить не менее трех раз и результаты занести в таблицу.
4. Нажать на клавишу "СБРОС" и проделать п.2 и п.3 для другого груза m2 при том же расстоянии h. 5. Для каждого измерения по формуле (4) вычислить момент силы M, а по формуле (6) - угловое ускорение b. При всех вычислениях обязательно следует учитывать массу платформы. В пределах погрешностей измерений убедиться в справедливости соотношения (7). Задание 2. Проверка соотношения: I2 – I1=M2 /b2 – M1 /b1 (8) Для этого случая момент инерции маятника различен, а момент силы, массы груза и радиус шкива постоянны. Момент инерции маятника можно изменить, закрепив груз m¢ в новом положении l2 относительно оси вращения маятника. Выведем уравнение, с помощью которого можно экспериментально проверить соотношение (8). Пусть I0 - момент инерции без грузов m¢, а I0- момент инерции всех четырех грузов общей массой 4m¢ относительно оси, проходящей через их центр масс. При удалении грузов m¢ на расстояние l от этой оси их момент инерции I¢ относительно новой оси, согласно теореме о переносе осей вращения (теорема Штейнера), будет равен I¢ = I¢0 +4m¢ l2 (9) Полный момент инерции маятника с грузами найдется по формуле I = I0 + I¢ или I = I0 + I0¢ + 4 m¢ l2 (10) для двух случаев размещения грузов m¢ на стержнях имеем: I1 = I0 + I0¢ + 4m¢ l2 I2 = I0 + I0¢ + 4m¢ l22 (11) если l2 > l1, то I2 - I1 = 4m¢ (l22 - l12). (12) С другой стороны, из основного закона динамики для вращательного движения (5) имеем: I2 – I1=M2 /b2 – M1 /b1 (13) Таким образом, уравнения (12) и (13) оказываются идентичными. Для проверки уравнения (13) необходимо: 1. Закрепить грузы m¢ симметрично в положении l2 > l1. 2. Провести те же измерения, что и в предыдущем задании и результаты занести в соответствующую таблицу. Положение l1 грузов m¢ и результаты измерений для этого случая берутся из табл.1. 3. По полученным экспериментальным данным проверить справедливость (в пределах ошибок измерений) формулы (12), а следовательно и формулы (13). Контрольные вопросы. 1. Определите угловое ускорение, момент силы и момент инерции. 2. Сформулируйте основной закон динамики для вращательного движения. 3. Объясните смысл проверки основного закона динамики для вращательного движения. 4. Объясните, как зависит инертность крестовины маятники Обербека от расположения грузов на стержнях? 5. Какая физическая величина характеризует эту инертность? РАБОТА №6.
Поиск по сайту: |
 где F-вращающая сила, R-плечо силы (в данном случае -радиус шкива).
где F-вращающая сила, R-плечо силы (в данном случае -радиус шкива).
 (2)
(2) (4)
(4) (6)
(6) Расстояние l от центра груза до оси вращения определяется (рис.2) по шкале, нанесенной на стержне, и определяется по формуле :
Расстояние l от центра груза до оси вращения определяется (рис.2) по шкале, нанесенной на стержне, и определяется по формуле :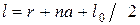



 1
1

