 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ И СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА
Приборы и принадлежности: прибор для определения внутреннего трения молекул воздуха, секундомер. Краткая теория Внутреннее трение (вязкость) связано с возникновением сил трения между слоями газа, перемещающимися параллельно друг другу с различными по величине скоростями. Эти силы направлены по касательной к поверхности слоев. Молекулы газа, переходя из одного слоя в другой, переносят импульс своего движения, в одном случае ускоряя это движение, в другом - замедляя его. Величина силы внутреннего трения F пропорциональна площади соприкосновения движущихся слоев S градиенту скорости где h - коэффициент внутреннего трения. Из формулы (1) следует, что коэффициент внутреннего трения в ед.СИ выражается в кг/ (м×с). Коэффициент внутреннего трения связан со средней длиной свободного пробега молекул газа соотношением где r - плотность газа при данной температуре , u - средняя арифметическая скорость молекул.
где m - молярная масса газа (для воздуха m = 28,9 кг/кмоль), P - давление газа, R - универсальная молярная газовая постоянная, равная 8,31 Дж/ (моль×К), Т - термодинамическая температура окружающей среды. Из формул (2) и (3) следует, что
Описание установки Для определения коэффициента внутреннего трения воздуха используется прибор, изображенный на рис.1
где t - время истечения воздуха, l - путь, проходимый за время t (длина капилляра), V - объем воздуха, прошедший через капилляр, r - радиус капилляра, DP - разность давлений на концах капилляра. Величина DP - рассчитывается по формуле DP = d×g×h, (6) где d - плотность жидкости, налитой в манометр, g - ускорение свободного падения, h - разность уровней в манометре. Выполнение работы Заполняют водой сосуд 1. Открывают кран 5, выжидают, пока установится стационарное течение (при этом разность уровней жидкости в манометре будет постоянной) и включают секундомер. После того, как вытечет определенный объем воды, выключают секундомер. По термометру определяют температуру Т, по барометру - давление P окружающей среды. По формулам (4) и (5) вычисляют Результаты измерений заносятся в табл.1. Таблица 1
Контрольные вопросы 1. Дайте определение длины свободного пробега молекул. От чего зависит длина свободного пробега молекул газа? 2. Как известно, воздух состоит из смеси газов. Что следует в этом случае понимать под средней длиной свободного пробега? 3. Почему коэффициент внутреннего трения жидкостей убывает с температурой, а у газов - возрастает? 4. Какие существуют скорости молекул газа? Расскажите о максвелловском законе распределения молекул по скоростям. РАБОТА № 9 ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ ПРОГИБА Принадлежности: станина с опорными призмами, индикатор с механизмом часового типа, линейка, штангенциркуль, набор стержней прямоугольного сечения. Краткая теория Все твердые тела характеризуются механическими свойствами, которыми определяется их способность изменять свою форму (деформироваться) под действием внешних механических сил. Деформация твердого тела является результатом изменения под действием внешней силы взаимного расположения частиц, из которых состоит тело, и расстояний между ними. Деформация называется упругой, если она исчезает после прекращения действия силы, и пластической, если она сохраняется и после прекращения нагрузки. Все твердые тела могут быть деформированы и упруго, и пластически. При малых силах твердые тела деформируются упруго. Рассмотрим более подробно упругую деформацию, которую всегда учитывают при расчете различных технических сооружений для их длительной работы. Как уже отмечалось, сила может деформировать твердое тело - смещать составляющие его частицы относительно друг друга. При этом (в соответствии с третьим законом Ньютона) внутри деформированного тела возникает противодействующая сила, равная по модулю деформирующей силе и называемая силой упругости. Эта сила стремится как бы восстановить первоначальную форму и объем твердого тела. Деформации, которые может испытывать твердое тело под действием приложенной внешней силы, сводятся к двум основным видам: растяжению или сжатию и сдвигу. Соотношение между силой упругости и деформацией определяется законом Гука: сила упругости F, возникающая при малых деформациях любого вида, пропорциональна деформации (смещению) где k - коэффициент пропорциональности, зависящий от вида деформации. Знак минус указывает на противоположность направлений силы упругости и смещения. При больших смещениях
Величина Е называется модулем Юнга или модулем упругости. Записав формулу закона Гука (2) в виде можно определить физический смысл модуля Юнга. Если в (3) положить ∆ℓ/ℓ=1 (т.е. удвоить длину), то В системе СИ модуль Юнга измеряется в Н/м2 (Па), а в системе СГС - в дин/см2. При одностороннем растяжении или сжатии изменяется не только длина стержня, но и его поперечные размеры, т.е. его радиус. Если эту деформацию характеризовать относительным изменением радиуса где М - коэффициент пропорциональности, который можно назвать модулем поперечного сжатия при продольном растяжении. Ясно, что между
Постоянная m называется коэффициентом Пуассона и равна отношению поперечного и продольного удлинений. Описание установки В нашей задаче метод определения модуля Юнга основан на измерении стрелы прогиба при деформации изгиба однородного стержня, лежащего на двух опорах, если к его середине приложена сосредоточенная сила Р. Если мысленно разбить стержень на тонкие продольные слои, то при изгибе его они окажутся различной длины. Нижние слои при этом удлиняются, верхние укорачиваются. Нейтральная линия среднего слоя сохраняет свою длину. Таким образом, деформация изгиба сводится к деформации одностороннего растяжения и сжатия. Перемещение, которое получит середина стержня под действием груза Р, называется стрелой прогиба l. Теоретические исследования деформации изгиба в нашем случае дают формулу для вычисления стрелы прогиба: где Р - вес груза, приложенный в центре стержня, Е - модуль Юнга, где m - масса груза, g - ускорение свободного падения.
Выполнение работы 1. Измерить линейкой расстояние L между опорными призмами. 2. Измерить штангенциркулем ширину 3. Нагрузить платформу последовательно грузами массой (1,0±0,001) кг и (0,5±0,01) кг. 4. Установить щуп индикатора таким образом, чтобы он касался рамки. 5. Совместить нуль шкалы со стрелкой индикатора. 6. Снять с платформы груз 0,5 кг и определить стрелу прогиба для этого груза. Повторить эту операцию трижды и взять среднее значение. 7. Проделать то же с грузом 1,0 кг. 8. Такие измерения провести с другим стержнем. 9. Данные опыта занести в таблицы, по формуле (7) вычислить модуль Юнга для каждого груза и погрешности измерений. Таблица данных измерений для первого стержня
Для другого стержня таблица аналогична. Контрольные вопросы 1. Сформулируйте и запишите закон Гука. 2. Запишите и объясните формулу закона Гука для деформаций растяжения и сдвига. 3. В чем физический смысл модуля Юнга и коэффициента Пуассона? 4. Объясните зависимость модуля Юнга от природы вещества и температуры. РАБОТА № 10
Поиск по сайту: |
 движения слоев и равна F= - h
движения слоев и равна F= - h  h =
h =  u
u  r, (2)
r, (2) Известно, что u =
Известно, что u =  и
и  , (3)
, (3) можно определить, зная h, P и Т:
можно определить, зная h, P и Т: ×
×  (4)
(4) Когда из сосуда 1 выливается вода, давление в нем понижается и через капилляр 2 из сосуда 3 в него засасывается воздух. Вследствие внутреннего трения давления на концах капилляра будут одинаковы. Разность этих давлений измеряется манометром 4. Коэффициент внутреннего трения воздуха при этом определяется формулой Пуазейля: h =
Когда из сосуда 1 выливается вода, давление в нем понижается и через капилляр 2 из сосуда 3 в него засасывается воздух. Вследствие внутреннего трения давления на концах капилляра будут одинаковы. Разность этих давлений измеряется манометром 4. Коэффициент внутреннего трения воздуха при этом определяется формулой Пуазейля: h =  , (5)
, (5)

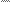 №
п/п
№
п/п




 , т.е.
, т.е.  (1)
(1) Под действием внешней силы длина стержня увеличится на некоторую величину ∆ℓ. Но это удлинение ∆ℓ не может быть принято за характеристику деформации, т.к. сила действует на каждую единицу длины ∆ℓ стержня, а длина стержня может быть разной. Поэтому удлинение ∆ℓ будет определяться не только действующей силой, но и первоначальной длиной стержня. В качестве величины деформации необходимо брать отношение ∆ℓ/ℓ, которое уже от ℓ не зависит. Это отношение называется относительным удлинением. Опыт показывает, что если в деформированном теле выделить некоторую произвольную поверхность, то деформация определяет не силу, действующую на эту поверхность, а отношение этой силы к площади поверхности
Под действием внешней силы длина стержня увеличится на некоторую величину ∆ℓ. Но это удлинение ∆ℓ не может быть принято за характеристику деформации, т.к. сила действует на каждую единицу длины ∆ℓ стержня, а длина стержня может быть разной. Поэтому удлинение ∆ℓ будет определяться не только действующей силой, но и первоначальной длиной стержня. В качестве величины деформации необходимо брать отношение ∆ℓ/ℓ, которое уже от ℓ не зависит. Это отношение называется относительным удлинением. Опыт показывает, что если в деформированном теле выделить некоторую произвольную поверхность, то деформация определяет не силу, действующую на эту поверхность, а отношение этой силы к площади поверхности  которая называется напряжением (измеряется она в тех же единицах, как и давление). Теперь закон Гука для одностороннего растяжения (а равно как и для сжатия, только с заменой знаков) можно записать в виде:
которая называется напряжением (измеряется она в тех же единицах, как и давление). Теперь закон Гука для одностороннего растяжения (а равно как и для сжатия, только с заменой знаков) можно записать в виде:  . (2)
. (2) (3)
(3) . Отсюда следует, что модуль Юнга Е численно равен напряжению s, которое растягивает стержень вдвое. Такое определение модуля Юнга носит отвлеченный характер, ибо в действительности линейная зависимость между деформацией и напряжением наблюдается только при малых деформациях
. Отсюда следует, что модуль Юнга Е численно равен напряжению s, которое растягивает стержень вдвое. Такое определение модуля Юнга носит отвлеченный характер, ибо в действительности линейная зависимость между деформацией и напряжением наблюдается только при малых деформациях  и подавляющее большинство материалов разрушается значительно раньше, чем будет достигнуто напряжение, численно равное модулю Юнга. Модуль Юнга - одна из существенных констант, характеризующих упругие свойства вещества.
и подавляющее большинство материалов разрушается значительно раньше, чем будет достигнуто напряжение, численно равное модулю Юнга. Модуль Юнга - одна из существенных констант, характеризующих упругие свойства вещества. , то можно записать
, то можно записать  (4)
(4) должна быть простая связь. Она выражается в том, что их отношение есть величина постоянная для данного вещества:
должна быть простая связь. Она выражается в том, что их отношение есть величина постоянная для данного вещества: . (5)
. (5) , (6)
, (6) - ширина,
- ширина,  - толщина, L - длина стержня. Из (6) следует формула для определения модуля Юнга
- толщина, L - длина стержня. Из (6) следует формула для определения модуля Юнга  (7)
(7) Прибор для определения модуля Юнга (рис.2) состоит из массивной станины 6 с двумя стойками, на концах которых имеются стальные опорные призмы 4, ребра которых параллельны. На ребра этих призм кладут испытуемый стержень 3, а к его середине подвешивают рамку 2, верхняя сторона которой представляет собой призму, обращенную ребром вниз. Этим ребром рамка опирается на стержень. Рамка несет на себе платформу 5 для гирь, с помощью которых создается изгибающая сила. На специальной стойке укрепляют индикатор 1, подводя его щуповой механизм к середине стержня до соприкосновения. Индикатор имеет механизм часового типа, в котором поступательное перемещение щупа преобразуется в заметный поворот стрелки индикатора. Индикатор имеет цену деления 0,01 мм и один оборот стрелки, равный 100 делениям, соответствует 1 мм поступательного движения щупа. Шкалу индикатора можно поворачивать, что дает возможность устанавливать против стрелки нуль шкалы при любом положении щупа.
Прибор для определения модуля Юнга (рис.2) состоит из массивной станины 6 с двумя стойками, на концах которых имеются стальные опорные призмы 4, ребра которых параллельны. На ребра этих призм кладут испытуемый стержень 3, а к его середине подвешивают рамку 2, верхняя сторона которой представляет собой призму, обращенную ребром вниз. Этим ребром рамка опирается на стержень. Рамка несет на себе платформу 5 для гирь, с помощью которых создается изгибающая сила. На специальной стойке укрепляют индикатор 1, подводя его щуповой механизм к середине стержня до соприкосновения. Индикатор имеет механизм часового типа, в котором поступательное перемещение щупа преобразуется в заметный поворот стрелки индикатора. Индикатор имеет цену деления 0,01 мм и один оборот стрелки, равный 100 делениям, соответствует 1 мм поступательного движения щупа. Шкалу индикатора можно поворачивать, что дает возможность устанавливать против стрелки нуль шкалы при любом положении щупа. мм
мм
 мм
мм
