 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ИССЛЕДОВАНИЕ ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА ПРИ ЦЕНТРАЛЬНОМ УДАРЕ ШАРОВ
Приборы и принадлежности: установка для изучения удара шаров, набор шаров. Краткая теория В механике под ударом понимается кратковременное взаимодействие двух тел, возникающее в результате их соприкосновения. Существуют два предельных случая удара – абсолютно упругийи абсолютно неупругий. При абсолютно упругом ударе механическая энергия соударяющихся тел не переходит во внутреннюю энергию, и, следовательно, полная механическая энергия системы : Wмех= Wкин + Wпот сохраняется. Идеальных абсолютно упругих ударов макроскопических тел не существует, так как часть их механической энергии всегда тратится на необратимую деформацию тел и увеличение их внутренней энергии (нагревание). Однако для некоторых тел (например, стальных шаров) потерями механической энергии можно пренебречь и рассматривать их удар как абсолютно упругий. При абсолютно неупругом ударе тела соединяются и после удара движутся как одно тело, масса которого равна сумме масс обоих тел: М = m1 + m2. Механическая энергия в этом случае не сохраняется, так как ее часть (или даже вся она целиком) переходит во внутреннюю энергию.
Удар называется центральным, если векторы скоростей соударяющихся тел лежат на прямой, соединяющей центры масс этих тел. Рассмотрим систему из двух шаров, подвешенных на практически нерастяжимых нитях (рис.). Отклоним шар с массой m1на угол a1от положения равновесия и отпустим его. В момент перед ударом его импульс равен m1v1.Второй шар при этом покоится и его импульс m2v2=0.В результате удара импульсы шаров изменятся и будут равны: m1v’1 и m2v’2. Поскольку удар центральный и векторы скоростей шаров лежат на одной прямой, то закон сохранения импульса можно записать в скалярной форме:
Если шары сталкиваются многократно, то после каждого соударения различие между их скоростями уменьшается и в результате после некоторого числа соударений шары начинают двигаться с одинаковой скоростью u, что эквивалентно неупругому соударению. При этом,согласно закону сохранения импульса Скорости шаров, входящие в формулы (2) и (3), могут быть найдены из закона сохранения энергии. Шар, отклоненный от положения равновесия на угол a, обладает потенциальной энергией: где h – высота подъема шара, которая, как следует из рис.1, равна: h = l (1 – cosa 1) = 2l sin2 a 1 ¤ 2, где l – длина нити подвеса. Когда шар 1 проходит через положение равновесия (т.е. в момент непосредственно перед соприкосновением шаров), его энергия (4) полностью (если пренебречь трением в подвесе и сопротивлением воздуха) перейдет в кинетическую энергию: откуда: По формуле (6), зная скорости шаров после удара: v1¢, v2¢ , u , можно определить углы a1¢, a2¢, a, на которые они отклонятся в результате удара, и наоборот, по известным углам можно найти скорости. Из второго закона Ньютона следует, что изменение импульса тела постоянной массы под действием внешней силы определяется соотношением:
Описание установки Конструкция установки, с помошью которой выполняется практическая часть работы, показана на рис.2. Каждый из шаров 1 подвешен на двух проводах 2, что обеспечивает движение обоих шаров в одной вертикальной плоскости и устраняет их вращение. На верхнем кронштейне имеется вороток 3, с помощью которого можно устанавливать между шарами требуемое расстояние. На нижнем кронштейне расположены угольники со шкалами 4, которые могут передвигаться, и электромагнит 5. На время соударения шаров замыкается электрическая цепь, позволяющая с помощью включенного в нее микросекундомера 6 измерять время, в течение которого шары находятся в контакте, т.е. время соударения. Выполнение рабаты На подвесы навинчиваются два шара. Воротком 3 на верхнем кронштейне, к которому подвешены шары, привести их в соприкосновение. Центры шаров (нанесенные на них круговые канавки) должны быть на одном уровне. Угольники со шкалами должны быть расположены так, чтобы острие каждого подвеса находилось против нулевого деления шкалы. Включить микросекундомер в сеть. Если требуется, отжать клавишу ПУСК и нажать клавишу СЕТЬ. Если на табло будут светиться цифры, то необходимо нажать клавишу СБРОС. При этом все индикаторы должны показывать цифру 0- прибор готов к работе. Примечание. Индикатор ПЕРЕПОЛНЕНИЕ не должен светиться. Перед началом измерений правый шар отводится на некоторый угол a1 так, чтобы он удерживался электромагнитом. Левый шар должен покоиться (a2 =0, v2 = 0). При нажатии клавиши ПУСК ток в цепи электромагнита выключается, шар освобождается и начинает двигаться. Происходит удар и микросекундомер показывает время Dt шаров. После соударения измеряется максимальный угол a2¢ отклонения левого шара в результате первого удара. После некоторого числа соударений шары начнут двигаться совместно с некоторой скоростью u . По одной из шкал измеряется угол a отклонения шаров при таком движении. Измерения величин a1, a2¢, a, Dt проводятся не менее 10 раз. После каждого измерения клавишей СБРОС производится обнуление микросекундомера. По средним значениям a1, a2¢ и a по формуле (5) рассчитываются скорости правого шара перед ударом v1, левого шара сразу после удара v2¢ и обоих шаров при их совместном движении u. Все данные заносятся в таблицу. Длина подвесов l измеряется линейкой.
По формуле (7), зная изменение импульса одного из шаров в результате удара и время соударения, можно определить среднюю силу, возникающую при соударении. Проведенные измерения позволяют определить изменение импульса DР2 левого шара, который до удара покоился: DР2 = m2v2¢ - m2v2 = m2v2¢ , и затем найти среднюю силу удара. Из сравнения импульса системы шаров до удара Р = m1v1 + m2v2 и их импульса при совместном движении после серии соударений Р¢ = (m1 + m2)u можно судить о выполнимости закона сохранения импульса. Результаты эксперимента не противоречат закону сохранения импульса Р = Р¢, только если разность импульсов ½Р - Р¢½ не превышает совместной ошибки их определения DР+DР ¢.
Абсолютные ошибки DР и DР ¢ проще рассчитать, если сначала вычислить относительные ошибки: 1.
2.
Зная относительные ошибки ЕР и ЕР¢ , можно определить абсолютные ошибки DР и DР¢ . Параметры шаров
Контрольные вопросы 1. Какая механическая система называется замкнутой (изолированной)? 2. Сформулируйте закон сохранения импульса. 3. Почему к явлению удара шаров можно применять закон сохранения импульса? 4. От чего зависит сила, возникающая при ударе. 5. Какие существуют разновидности удара? РАБОТА № 8
Поиск по сайту: |
 При любом ударе систему из двух соударяющихся тел можно считать замкнутой (изолированной), поскольку взаимодействие между этими телами при ударе намного превосходит их взаимодействие со всеми другими телами, которым можно пренебречь. Следовательно, при любом ударе выполняется закон сохранения импульса:
При любом ударе систему из двух соударяющихся тел можно считать замкнутой (изолированной), поскольку взаимодействие между этими телами при ударе намного превосходит их взаимодействие со всеми другими телами, которым можно пренебречь. Следовательно, при любом ударе выполняется закон сохранения импульса:  (1)
(1) (2)
(2)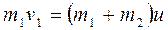 (3)
(3) , (4)
, (4) , (5)
, (5)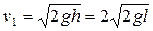
 . (6)
. (6) (7)
(7) Если рассматривать эту формулу применительно к удару, то
Если рассматривать эту формулу применительно к удару, то 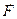 - это средняя сила удара за время ее действия Dt, т.е. за время соприкосновения соударяющихся тел, m – масса одного из тел,
- это средняя сила удара за время ее действия Dt, т.е. за время соприкосновения соударяющихся тел, m – масса одного из тел,  - изменение скорости этого тела, возникшее в результате удара. Из (7) следует, что при фиксированном изменении скорости сила удара тем больше, чем меньше время соударения.
- изменение скорости этого тела, возникшее в результате удара. Из (7) следует, что при фиксированном изменении скорости сила удара тем больше, чем меньше время соударения. Dt, мкс
Dt, мкс
 .10
.10






 или:
или:  . Тогда:
. Тогда:
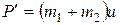 , или:
, или:  . Тогда:
. Тогда: .
.