Математический маятник

Математическим маятником называют систему, состоящую из невесомой и нерастяжимой нити, на которой подвешен шарик, масса шарика сосредоточена в одной точке (рис.3). В положении равновесия на шарик действуют две силы: сила тяжести P=mg и сила натяжения нити N - равные по величине и направленные в противоположные стороны.

Если маятник отклонить от положения равновесия на небольшой угол α, то он начнет совершать колебания в вертикальной плоскости под действием составляющей силы тяжести P_t, которую называют тангенциальной составляющей (нормальная составляющая силы тяжести P_n будет уравновешиваться силой натяжения нити N).

Из рис.3 видно, что тангенциальная составляющая силы тяжести .

Знак минус показывает, что сила, вызывающая колебательное движение, направлена в сторону уменьшения угла α. Если угол α мал, то синус можно заменить самим углом, тогда .

С другой стороны, из рис.3 видно, что угол α можно записать через длину дуги x и радиус ℓ: α = x/ℓ, т.е. сила, возвращающая маятник в положение равновесия, является квазиупругой: , где - коэффициент квазиупругой силы. Второй закон Ньютона в этом случае будет иметь следующий вид: . (7)

С учетом (4), можно записать, что , откуда . (8)

Период колебаний математического маятника при малых углах отклонения

не зависит от амплитуды колебания и от его массы, а определяется длиной маятника и ускорением свободного падения g.

Физический маятник

Физическим маятником называется абсолютно твердое тело, которое может совершать колебания под действием силы тяжести вокруг горизонтальной оси О, перпендикулярной плоскости рисунка и не проходящей через его центр тяжести.

На рис.4 изображено сечение физического маятника плоскостью, перпендикулярной к его оси вращения О и проходящей через его центр тяжести С.

Запишем в общем виде уравнение движения маятника, т.е. основное уравнение динамики вращательного движения

M = Jβ, (9)

где J - момент инерции маятника относительно горизонтальной оси О, β - угловое ускорение, М - момент внешних сил. В нашем случае момент внешних сил обусловлен действием силы тяжести. Очевидно, что на каждый элемент массы Δm_i маятника действует сила тяжести Δm_ig, создающая определенный момент

относительно оси О. Сумма моментов этих сил равна моменту равнодействующей сил тяжести, которая приложена к центру тяжести маятника (точка С).

Докажем, что маятник, выведенный из положения равновесия на малый угол φ, будет совершать гармонические колебания. Для этого равнодействующую сил тяжести P=mg разложим на две составляющие, одна из которых P₂ уравновешивается реакцией опоры, а под действием другой составляющей P₁=Psinφ маятник приходит в движение. Обозначим расстояние от точки подвеса О до центра тяжести С через a. Тогда уравнение движения маятника (9) запишется в виде

Jβ=-P₁·a=-P·a·sinφ. (10)

Знак минус показывает, что сила P₁ направлена к положению равновесия и приводит к уменьшению угла отклонения φ. Так как , а для малых углов φ можно принять sinφ≈φ, то уравнение (10) будет иметь вид:

, или . (11)

Частным решением этого дифференциального уравнения является уравнение

, где . Исходя из полученного выражения для ω, находим выражение для периода колебаний физического маятника

. (12)

Величина называется приведенной длиной физического маятника, это есть длина эквивалентного математического маятника, имеющего тот же период колебаний, что и данный физический маятник.

Физическим маятником также можно воспользоваться для определения ускорения свободного падения.

Любой физический маятник обладает свойством сопряженности, которое заключается в том, что в нем можно найти такие две точки, что при последовательном подвешивании маятника за ту или иную из них, период колебаний его остается одним и тем же. Расстояние между этими точками определяет собой приведенную длину физического маятника.

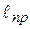Разновидностью физического маятника является оборотный маятник, который обладает свойством сопряженности центра качания и точки подвеса. Центром качания называется точка, находящаяся на расстоянии приведенной длины от оси вращения. Приведенная длина всегда больше величины a (см.рис.4), т.е. центр качания всегда лежит ниже центра тяжести. Действительно, по теореме Штейнера момент инерции маятника относительно оси вращения равен J=J_o+ma², где J_o - момент инерции маятника относительно оси, проходящей через центр тяжести. Тогда приведенная длина ℓ_пр равна , т.е. >a.

РАБОТА N 2-1

Поиск по сайту: