 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРОВЕРКА ЗАКОНОВ КОЛЕБАНИЯ МАТЕМАТИЧЕСКОГО МАЯТНИКА
И ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ Приборы и принадлежности: математический маятник, секундомер, штангенциркуль. Описание установки В качестве математического маятника в работе используется тяжелый металлический шарик 1, подвешенный на длинной тонкой нити (рис.1). Длина нити может меняться путем перемещения крепящего кронштейна 2 вдоль нити и измеряется по шкале 3, амплитуда колебаний маятника измеряется по шкале 4. При выполнении данной работы необходимо определение длины математического маятника и его периода колебаний.
Период колебаний определяется секундомером и его время рассчитывается из 20-30 полных колебаний маятника по формуле T = t/n (2), где t – время n полных колебаний Целью работы является изучение зависимости периода колебаний математического маятника от длины и амплитуды колебаний. Как следует из теории математического маятника, период его колебаний определяется по формуле
Тогда, очевидно, для разных длин маятника Для проверки этого соотношения кронштейном 2 установите длину маятника 140-150 см и определите его период колебаний. Затем, передвигая кронштейн, уменьшите длину маятника вдвое и опять определите период колебаний. Измерения проводятся не менее трех раз и данные заносятся в таблицу1.
Сделайте вывод о характере зависимости периода колебаний математического маятника от его длины. Для проверки зависимости периода колебаний от амплитуды колебаний установите фиксированную длину маятника, отклоните шарик примерно на 5 см и определите период его колебаний. Удвойте амплитуду колебаний и снова определите период колебаний. Для каждой амплитуды А период колебаний Т рекомендуется определять не менее трех раз, а затем вычислить среднее значение. Максимальное значение амплитуды не должно превышать 20-25 см. Составьте таблицу, аналогичную предыдущей, все данные занесите в эту таблицу и на основании полученных результатов сделайте вывод о характере зависимости периода колебаний математического маятника от амплитуды его колебаний. При определении ускорения свободного падения необходимо учитывать следующее. Так как длиной математического маятника является расстояние от точки подвеса до его центра тяжести, а центр тяжести лабораторного математического маятника не совпадает точно с геометрическим центром шарика, то непосредственное точное измерение длины не представляется возможным. Поэтому при определении ускорения свободного падения наблюдают колебания маятника для разных длин ℓ1 и ℓ2, определяя Т1 и Т2 , и находят g по формуле, полученной из (3):
Расстояния ℓ 1 и ℓ 2 и соответствующие им значения Т1 и Т2 можно взять из проделанных выше опытов. С целью оценки погрешности вычисления ускорения свободного падения выведите формулу для расчета абсолютной и относительной ошибок измерения и определите их ( Контрольные вопросы 1. Какой колебательный процесс называется гармоническим и каково его аналитическое и графическое представление? 2. Перечислите характеристики гармонического колебания, определите их физический смысл. 3. По какому закону изменяются при гармонических колебаниях смещение, скорость и ускорение? 4. От каких величин зависит ускорение свободного падения? ЗАТУХАЮЩИЕ КОЛЕБАНИЯ Простейшим видом колебательного движения является гармоническое, которое совершается по закону синуса или косинуса. Оно возникает в том случае, если на тело, выведенное из положения равновесия, непрерывно действует сила, направленная всегда к положению равновесия, а по величине пропорциональная смещению этого тела от положения равновесия.
Если колебательное движение происходит в какой-либо внешней среде, то эта среда оказывает сопротивление движению, стремясь замедлить его. Такой процесс движения можно описать, если ввести дополнительную силу, появляющуюся в результате самого движения и направленную противоположно ему. Такой силой является сила трения. Рассмотрим такое колебательное движение шарика, подвешенного на упругой пружине (рис.1). После отклонения шарика от положения равновесия он будет совершать гармонические колебания. Если деформация пружины невелика, то можно считать справедливым закон Гука и записать выражение для возвращающей в равновесие шарик силы F в виде: где k – коэффициент пропорциональности, зависящий от упругих свойств пружины, x – смещение относительного положения равновесия. Знак минус показывает, что сила направлена к положению равновесия, т.е. имеет знак, обратный знаку x. Под влиянием этой силы предоставленный самому себе шарик начнет двигаться, приобретая скорость где r – коэффициент пропорциональности, называемый коэффициентом сопротивления (коэффициент трения). Если масса шарика невелика (это дает возможность пренебречь силой тяжести по сравнению с возникающими упругими силами), то второй закон Ньютона будет иметь вид: После преобразований Здесь
Уравнение (4) есть дифференциальное уравнение затухающих колебаний, и решение которого имеет вид Здесь: А0 – амплитуда колебаний в начальный момент времени;
А период колебаний Т будет В формулу (5) входят два множителя, зависящие от времени. Один coswt – периодическая функция времени, другой е-dt - убывает с течением времени, Тогда, если коэффициент сопротивления мал, то величину А=А0е–dt можно рассматривать как амплитуду, которая с течением времени уменьшается по экспоненциальному закону, окончательно решение уравнения затухающих колебаний можно записать в общем виде:
Графически затухающие колебания представлены на рис.2. Из формулы Итак, возьмем отношение двух амплитуд Аn и An+1 (см. рис.2)
Величина D называется декрементом затухания. Чем больше декремент затухания, тем скорее уменьшается амплитуда. Чаще затухающие колебания характеризуются логарифмическим декрементом затухания q:: Таким образом, для характеристики затухающих колебаний вводятся две величины: коэффициент затухания d и логарифмический декремент затухания q . Поясним их физический смысл. Обозначим через t промежуток времени, за который амплитуда колебаний уменьшится в е раз. Тогда Следовательно, коэффициент затухания d есть физическая величина обратная промежутку времени t, в течение которого амплитуда убывает в е раз. Величина t называется временем релаксации. Если, например, d= 10 2 с. , то это значит, что амплитуда колебаний убывает в е раз за время 10 2 с. Пусть n – число колебаний, после которых амплитуда уменьшается в е раз. Тогда t = nT и q = dТ = 1/t = 1/n. Следовательно, логарифмический декремент затухания q есть физическая величина, обратная числу колебаний n, по истечении которого амплитуда убывает в е раз. Если, например, q = 0,01, то это значит, что амплитуда колебаний убывает в е раз по истечении 100 колебаний. РАБОТА № 3-1
Поиск по сайту: |
 Длина математического маятника ℓ находится как сумма длины нити ℓ1 от положения кронштейна до шарика (измерения проводятся по миллиметровой шкале) и радиуса шарика r = d/ℓ (измерения проводятся с помощью штангенциркуля). Таким образом, длина математического маятника будет равна: ℓ=ℓ1+d/2 (1)
Длина математического маятника ℓ находится как сумма длины нити ℓ1 от положения кронштейна до шарика (измерения проводятся по миллиметровой шкале) и радиуса шарика r = d/ℓ (измерения проводятся с помощью штангенциркуля). Таким образом, длина математического маятника будет равна: ℓ=ℓ1+d/2 (1) . (3)
. (3) 1 и
1 и 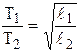 . (4)
. (4) =…
=…
 =…
=…



 (5).
(5). =2 мм, а ΔΤ берется из эксперимента).
=2 мм, а ΔΤ берется из эксперимента). Колебательные движения системы имеют особенно простой характер в случае малых колебаний, когда мало смещение системы от положения равновесия. Примером простейших колебательных систем может служить небольшое тело (шарик), подвешенное на пружине или нити (математический маятник).
Колебательные движения системы имеют особенно простой характер в случае малых колебаний, когда мало смещение системы от положения равновесия. Примером простейших колебательных систем может служить небольшое тело (шарик), подвешенное на пружине или нити (математический маятник). , (1)
, (1) . При его движении возникает сила трения Fтр , направленная противоположно скорости. В первом приближении ее можно считать пропорциональной скорости шарика:
. При его движении возникает сила трения Fтр , направленная противоположно скорости. В первом приближении ее можно считать пропорциональной скорости шарика:  , (2),
, (2), . (3)
. (3) . Или
. Или  . (4)
. (4) - квадрат собственной частоты колебаний шарика, т.е. колебаний при отсутствии сил трения и других внешних сил;
- квадрат собственной частоты колебаний шарика, т.е. колебаний при отсутствии сил трения и других внешних сил; , где δ - называется коэффициентом затухания.
, где δ - называется коэффициентом затухания. . (5)
. (5) - циклическая частота затухающих колебаний, е – основание натурального логарифма (е= 2,71).
- циклическая частота затухающих колебаний, е – основание натурального логарифма (е= 2,71). (6)
(6) . (7)
. (7) Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Поэтому величины w и Т называть частотой и периодом можно только условно.
Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Поэтому величины w и Т называть частотой и периодом можно только условно. , выражающей закон убывания амплитуды колебаний, можно показать, что отношение амплитуд, отделенных друг относительно друга интервалом в один период Т, остается постоянным в течение всего процесса затухания.
, выражающей закон убывания амплитуды колебаний, можно показать, что отношение амплитуд, отделенных друг относительно друга интервалом в один период Т, остается постоянным в течение всего процесса затухания. (8)
(8) , или q = d Т (9)
, или q = d Т (9) , откуда dt=1 или
, откуда dt=1 или  .
.