 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Признаки Даламбера и Коши для знакопеременных рядов⇐ ПредыдущаяСтр 12 из 12
Пусть дан знакопеременный ряд. Признак Даламбера. Если существует предел Признак Коши. Если существует предел
Практическое занятие №30 Наименование занятия: Нахождение области сходимости степенного ряда. Разложение элементарных функций в ряд Маклорена Цель занятия:Научиться находить область сходимости степенных рядов, раскладывать элементарные функции в ряд Маклорена. Подготовка к занятию:Повторить теоретический материал по теме «Теория рядов». Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Степенные ряды
Степенным рядомназывается ряд вида
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример 1. Исследовать на сходимость ряд Решение. Применяем признак Даламбера:
Получаем, что этот ряд сходится при Теперь определим сходимость в граничных точках 1 и –1. При х = 1: При х = -1: Теорема Абеля. Если степенной ряд Следствие. Если при х = х1 ряд расходится, то он расходится для всех
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
Пример 2. Найти область сходимости ряда Решение. Находим радиус сходимости ряда
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
Теорема. Если степенной ряд
Поиск по сайту: |
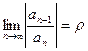 , то при r<1 данный ряд будет абсолютно сходящимся, а при r>1 - расходящимся. При r=1 признак не дает ответа о сходимости ряда.
, то при r<1 данный ряд будет абсолютно сходящимся, а при r>1 - расходящимся. При r=1 признак не дает ответа о сходимости ряда. , то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
, то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.




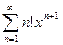







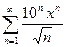





















 .
.
 .
. и расходится при
и расходится при  .
. ряд сходится по признаку Лейбница
ряд сходится по признаку Лейбница ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд). .
. ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.

 .
.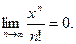
 сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри
сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри  .
.