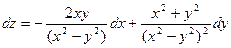|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Функций нескольких переменных
Цель занятия:Научиться находить частные производные и дифференциалы функций нескольких переменных. Подготовка к занятию:Повторить теоретический материал по теме «Дифференциальное исчисление функции нескольких действительных переменных». Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Производные функций нескольких переменных Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х. Можно записать
Тогда Обозначается: Аналогично определяется частная производная функции по у.
Пример 1. Найти частные производные функции
Пример 2. Найдем частные производные функции
Полное приращение и полный дифференциал Выражение
Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).
Для функции произвольного числа переменных:
Пример 3. Найти полный дифференциал функции
Пример 4. Найти полный дифференциал функции
Поиск по сайту: |


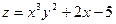




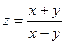







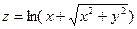












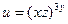







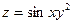







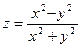
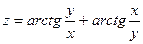

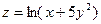

 , если
, если 
 , если
, если 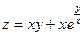
 , если
, если 
 , если
, если 
 , если
, если 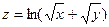
 .
. называется частной производнойфункции z = f(x, y) по х.
называется частной производнойфункции z = f(x, y) по х.
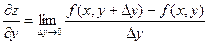
 .
. ,
,  .
.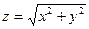 :
: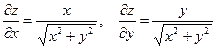 .
.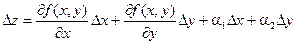 называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.

 .
.