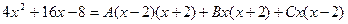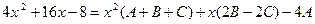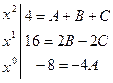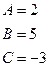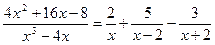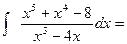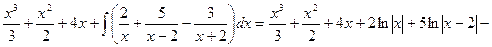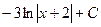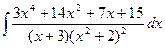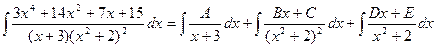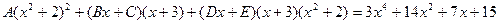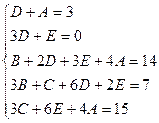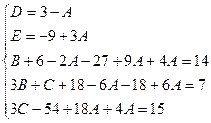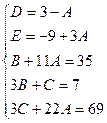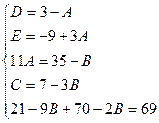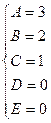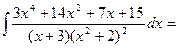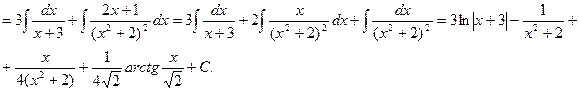|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование функций, содержащих квадратный трехчлен
Интегрирование функций, содержащих квадратный трехчлен сводится к выделению полного квадрата из квадратного трехчлена. Пример 1. Вычислить интеграл Решение. Выделим их квадратного трехчлена полный квадрат:
Пример 2. Вычислить интеграл Решение. Т.к.
Интегрирование рациональных дробей
Для того чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины. При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х. Пример 2. Вычислить интеграл Решение. Правильную дробь
Пример 3. Вычислить интеграл Решение. Подынтегральная функция является неправильной дробью, поэтому сначала выделим её целую часть делением многочлена на многочлен:
Тогда
Правильную дробь
Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений для нахождения коэффициентов A, B, C.
Таким образом, Подставив получившееся разложение в заданный интеграл, получим:
Пример 4. Вычислить интеграл Решение. Разложим подынтегральную функцию на простейшие дроби и найдем неопределенные коэффициенты.
Тогда значение заданного интеграла будет равно:
Практическое занятие №19 Наименование занятия: Интегрирование иррациональных функций. Универсальная подстановка Цель занятия:Научиться вычислять неопределенные интегралы от рациональных и иррациональных функций. Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной». Литература:
Задание на занятие:
Поиск по сайту: |
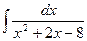
 . Тогда
. Тогда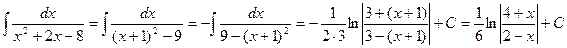
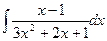
 ,
, 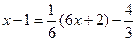 , то
, то 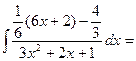
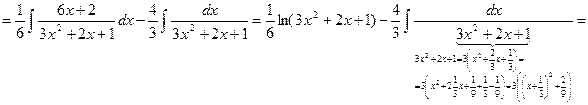
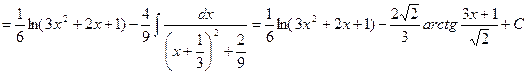

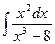
 разложим на простейшие дроби.
разложим на простейшие дроби.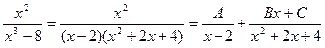
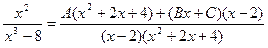
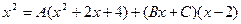
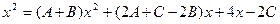

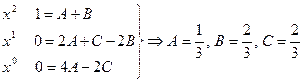
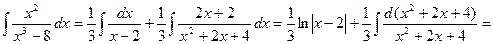
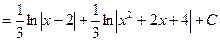
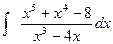 .
.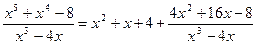 ;
;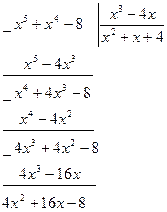
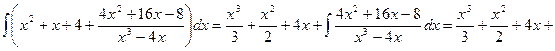
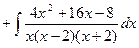
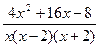 разложим на простейшие дроби и найдём коэффициенты A, B, C.
разложим на простейшие дроби и найдём коэффициенты A, B, C. приведя правую часть равенства к общему знаменателю и отбросив последний, имеем:
приведя правую часть равенства к общему знаменателю и отбросив последний, имеем: