 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Доказать расходимость рядов, используя следствие из необходимого признака сходимости
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Понятие числового ряда Числовым рядомназывается выражение вида:
При этом числа Примеры рядов Из членов бесконечной геометрической прогрессии можно составить ряд:
Если, например, взять a = 1, q =
Ряд
Сумма первых п членов ряда называется частичной суммой ряда. Таким образом, с рядом (1) связывается последовательность его частичных сумм S1, S2, …,Sn, …, где S1 = а1, S2 = а1 + а2, … Sn = а1 + а2 + … + ап, … Ряд
Число S называется суммой ряда.
Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся. Например, ряд геометрической прогрессии Гармонический ряд Свойства рядов Теорема 1. Если ряд
Другими словами: сходимость (расходимость) ряда не нарушится, если все его члены умножить на одно и то же отличное от нуля число. Теорема 2. Если ряды Другими словами: сходящиеся ряды можно почленно складывать и вычитать. Следствие: Сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд. Теорема 3. Если в ряде
Поиск по сайту: |
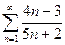
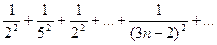
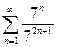
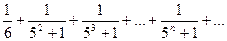
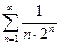
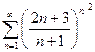
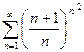
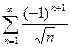
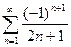
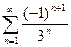
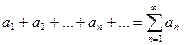(1)
называются членами ряда (1), аn – общим членом ряда.
- ряд геометрической прогрессии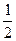
, то получим ряд:
называется гармоническим рядом.
называется сходящимся, если сходится последовательность его частных сумм, т.е. если существует предел
.
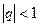. Если 
, то этот ряд сходится только при а = 0, а в остальных случаях расходится.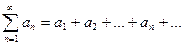
(1) сходится и его сумма равна S, то для произвольного числа с ряд 
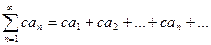(2) тоже сходится, и его сумма равна сS. Если же ряд (1) расходится и с ≠ 0, то и ряд (2) расходится.
(3) сходятся и их суммы равны соответственно S1 и S3, то и каждый из двух рядов 
сходится и его сумма равна соответственно S1 ± S3.