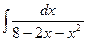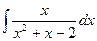|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование по частям
Этот метод применяется, когда подынтегральная функция имеет вид:
где u и dv выбираются в соответствии с правилами: 1. Если 2. Если 3. Интегралы вида
Пример 6. Вычислить Решение. Данный интеграл относится к 1 типу. Положим
Пример 7. Вычислить Решение. Данный интеграл относится ко 2 типу. Выполним замену:
Пример 8. Вычислить Решение. Данный интеграл относится к 1 типу. Выполним замену:
(Получили интеграл, который решается интегрированием по частям. Выполним замену еще раз:
Пример 9. Вычислить
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
Практическое занятие №18 Наименование занятия: Интегрирование рациональных функций Цель занятия:Научиться вычислять неопределенные интегралы от рациональных функций Подготовка к занятию:Повторить теоретический материал по теме «Интегральное исчисление функции одной действительной переменной» Литература:
Задание на занятие:
Вычислить неопределенные интегралы
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Поиск по сайту: |
 , где
, где  - это многочлен степени п, а
- это многочлен степени п, а  является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией. Формула метода:
является показательной, тригонометрической, обратной тригонометрической или логарифмической функцией. Формула метода: ,
, ,
,  ,
,  ), то для того чтобы найти эти интегралы, нужно сделать замену
), то для того чтобы найти эти интегралы, нужно сделать замену 
 и применить формулу интегрирования по частям.
и применить формулу интегрирования по частям. ,
,  ,
,  ,
,  ,
,  ) то для того, чтобы найти эти интегралы нужно сделать замену:
) то для того, чтобы найти эти интегралы нужно сделать замену:  ,
,  .
. ,
,  (a, b — числа) вычисляются двукратным интегрированием по частям.
(a, b — числа) вычисляются двукратным интегрированием по частям. .
. ,
,  ; тогда
; тогда  ,
,  . Подставим в формулу интегрирования по частям:
. Подставим в формулу интегрирования по частям: .
.
 ,
,  ,
,  ,
, 


 ,
,  ,
,  ,
, 

 ,
,  ,
, 
 .
.